School of Computing - Learning Python

Module 21. Trees

Learning Objectives

Understand the trade-offs between different tree data structures in terms of performance and memory usage.
Define trees and their key components (nodes, edges, root, leaves, branches, subtrees).
Explain the different types of trees (binary trees, binary search trees, AVL trees, heaps).
Implement basic tree operations (creating, traversing, searching, inserting, and deleting) using Python.
Analyze the time and space complexity of tree algorithms.
Apply trees to solve real-world problems, such as data structures for efficient searching and sorting.

1. Introduction

Trees are a fundamental data structure in computer science that can be used to represent hierarchical relationships between elements. Think of a tree as an upside-down family tree, where the root node is at the top and the leaves are at the bottom.

In Python, trees can be implemented using various techniques, including:

Using nested lists to represent the hierarchical structure.
Creating custom classes to define nodes and their relationships.
Leveraging built-in data structures like dictionaries or collections.

This module will explore the concepts of trees in Python, focusing on their definition, types, operations, and applications.

2. Types of Trees

Binary Trees

Binary search trees (BSTs): A binary tree where the left child of a node has a value less than the parent, and the right child has a value greater than the parent.
AVL trees: A self-balancing binary search tree where the heights of the left and right subtrees of any node differ by at most one.
Heaps: A complete binary tree where either all nodes are greater than or equal to their children (max heap), or all nodes are less than or equal to their children (min heap).

Other Tree Types

Red-Black trees: a red–black tree is a self-balancing binary search treedata structure noted for fast storage and retrieval of ordered information.
General trees: Trees where nodes can have an arbitrary number of children.
N-ary trees: Trees where each node has at most N children.
Trie: A tree-like data structure used for efficient string searching.
Suffix tree: A trie that stores all suffixes of a string.
Decision trees: Trees used in machine learning to make decisions based on a set of rules.

These are just a few examples of the many types of trees that exist. The choice of tree data structure depends on the specific requirements of the problem at hand.

3. Binary Trees

Binary trees are a specific type of tree where each node has at most two children. They are commonly used in computer science due to their simplicity and efficiency.

Key Concepts

Node: A basic unit of a binary tree, containing a value and pointers to its left and right children.
Root: The topmost node in a binary tree.
Leaf: A node with no children.
Internal node: A node with at least one child.
Subtree: A connected subset of a binary tree that is itself a binary tree.

Types of Binary Trees

Full binary tree: Every node has either 0 or 2 children.
Complete binary tree: All levels are filled except possibly the last, and all nodes on the last level are as far left as possible.
Perfect binary tree: A full binary tree where all leaves are at the same depth.

Traversal Algorithms

There are three common ways to traverse a binary tree:

In-order traversal: Visit the left subtree, then the root, then the right subtree.

In in-order traversal, the left child is visited first, followed by the node itself, and then the right child. This can be visualized as Left - Root - Right.

Output:

In-Order Traversal: 4 2 5 1 3

Pre-order traversal: Visit the root, then the left subtree, then the right subtree.

In pre-order traversal, the node is visited first, followed by its left child and then its right child. This can be visualized as Root - Left - Right.

Output:

Pre-Order Traversal: 1 2 4 5 3

Post-order traversal: Visit the left subtree, then the right subtree, then the root.

In post-order traversal, the left child is visited first, then the right child, and finally the node itself. This can be visualized as Left - Right - Root.

Output:

Post-Order Traversal: 4 5 2 3 1

3.1 Binary Search Tree

A Binary Search Tree (or BST) is a data structure used in computer science for organizing and storing data in a sorted manner. Each node in a Binary Search Tree has at most two children, a left child and a right child, with the left child containing values less than the parent node and the right child containing values greater than the parent node. This hierarchical structure allows for efficient searching, insertion, and deletion operations on the data stored in the tree.

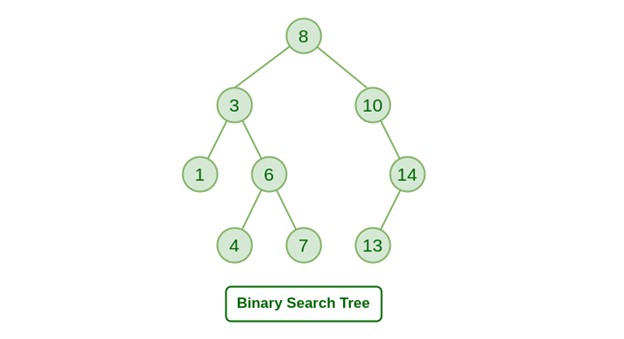
Insertion in Binary Search Tree (BST)

Given a BST, the task is to insert a new node in this BST.

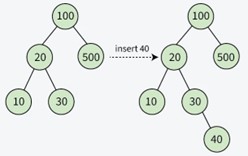
How to Insert a value in a Binary Search Tree:

A new key is always inserted at the leaf by maintaining the property of the binary search tree. We start searching for a key from the root until we hit a leaf node. Once a leaf node is found, the new node is added as a child of the leaf node. The below steps are followed while we try to insert a node into a binary search tree:

Initilize the current node (say, currNode or node) with root node
Compare the key with the current node.
Move left if the key is less than or equal to the current node value.
Move right if the key is greater than current node value.
Repeat steps 2 and 3 until you reach a leaf node.
Attach the new key as a left or right child based on the comparison with the leaf node’s value.

Insertion in Binary Search Tree using Recursion:

Below is the implementation of the insertion operation using recursion.

Output:

20 30 40 50 60 70 80

Time Complexity: The worst-case time complexity of insert operations is O(h) where h is the height of the Binary Search Tree.

In the worst case, we may have to travel from the root to the deepest leaf node. The height of a skewed tree may become n and the time complexity of insertion operation may become O(n).

Insertion in Binary Search Tree using Iterative approach:

Instead of using recursion, we can also implement the insertion operation iteratively using a while loop. Below is the implementation using a while loop.

# Python program to demonstrate
# insert operation in binary search tree
class Node:
    def __init__(self, key):
        self.left = None
        self.right = None
        self.key = key

def insert(root, key):
    temp = Node(key)

# If tree is empty
    if root is None:
        return temp

# Find the node who is going to 
    # have the new node temp as its child
    parent = None
    curr = root
    while curr is not None:
        parent = curr
        if curr.key > key:
            curr = curr.left
        elif curr.key < key:
            curr = curr.right
        else:
            return root  # Key already exists

# If key is smaller, make it left 
    # child, else right child
    if parent.key > key:
        parent.left = temp
    else:
        parent.right = temp

return root

# A utility function to do inorder tree traversal
def inorder(root):
    if root:
        inorder(root.left)
        print(root.key, end=" ")
        inorder(root.right)

# Creating the following BST
#      50
#     /  \
#    30   70
#   / \   / \
#  20 40 60 80
r = Node(50)
r = insert(r, 30)
r = insert(r, 20)
r = insert(r, 40)
r = insert(r, 70)
r = insert(r, 60)
r = insert(r, 80)

# Print inorder traversal of the BST
inorder(r)

Output:

20 30 40 50 60 70 80

The time complexity of inorder traversal is O(n), as each node is visited once.

The Auxiliary space is O(n), as we use a stack to store nodes for recursion.

Searching in Binary Search Tree:

The task is to search a node in this BST. For searching a value in BST, consider it as a sorted array. Now we can easily perform search operation in BST using Binary Search Algorithm. (Binary Search Algorithm: below is the step-by-step algorithm for Binary Search: Divide the search space into two halves by finding the middle index “mid”. Compare the middle element of the search space with the key. If the key is found at middle element, the process is terminated. If the key is not found at middle element, choose which half will be used as the next search space. If the key is smaller than the middle element, then the left side is used for next search. If the key is larger than the middle element, then the right side is used for next search. This process is continued until the key is found or the total search space is exhausted.)

Input: Root of the below BST

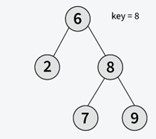
Output: True
Explanation: 8 is present in the BST as right child of root

Input: Root of the below BST

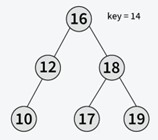
Output: False
Explanation: 14 is not present in the BST

Output:

19 is Not Found20 is Found

Time complexity: O(h), where h is the height of the BST.

Deletion in Binary Search Tree: the task is to delete a node in this BST, which can be broken down into 3 scenarios:

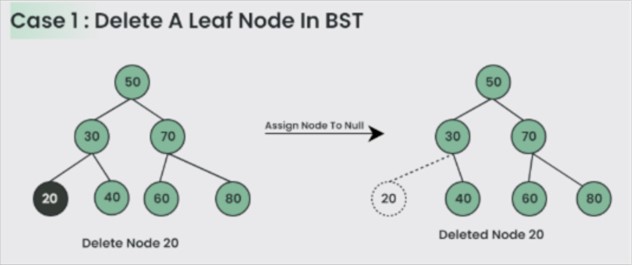
Case1: Delete a Leaf Node in BST

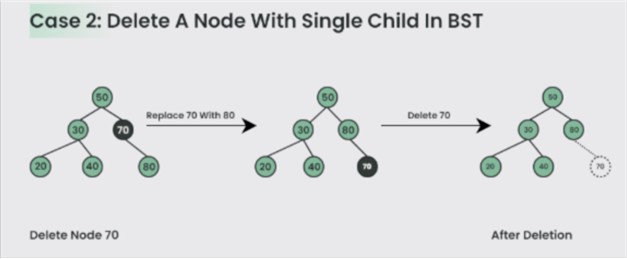
Case2: Delete a Node with Single Child in BST

Deleting a single child node is also simple in BST. Copy the child to the node and delete the node.

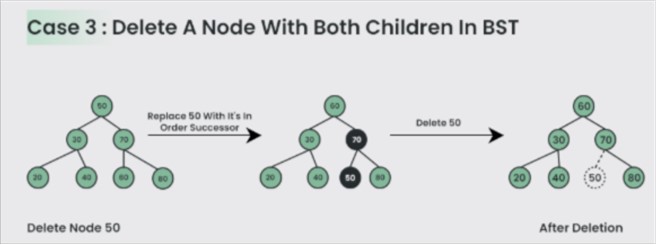
Case3: Delete a Node with Both Children in BST

Deleting a node with both children is not so simple. Here we have to delete the node is such a way, that the resulting tree follows the properties of a BST. The trick is to find the inorder successor of the node. Copy contents of the inorder successor to the node, and delete the inorder successor.

class Node:
    def __init__(self, key):
        self.key = key
        self.left = None
        self.right = None

# Note that it is not a generic inorder successor 
# function. It mainly works when the right child
# is not empty, which is  the case we need in BST
# delete.
def get_successor(curr):
    curr = curr.right
    while curr is not None and curr.left is not None:
        curr = curr.left
    return curr

# This function deletes a given key x from the
# given BST and returns the modified root of the 
# BST (if it is modified).
def del_node(root, x):
  
    # Base case
    if root is None:
        return root

# If key to be searched is in a subtree
    if root.key > x:
        root.left = del_node(root.left, x)
    elif root.key < x:
        root.right = del_node(root.right, x)
        
    else:
        # If root matches with the given key

# Cases when root has 0 children or 
        # only right child
        if root.left is None:
            return root.right

# When root has only left child
        if root.right is None:
            return root.left

# When both children are present
        succ = get_successor(root)
        root.key = succ.key
        root.right = del_node(root.right, succ.key)
        
    return root

# Utility function to do inorder traversal
def inorder(root):
    if root is not None:
        inorder(root.left)
        print(root.key, end=" ")
        inorder(root.right)

# Driver code
if __name__ == "__main__":
    root = Node(10)
    root.left = Node(5)
    root.right = Node(15)
    root.right.left = Node(12)
    root.right.right = Node(18)
    x = 15

root = del_node(root, x)
    inorder(root)
    print()

Output:

5 10 12 18

Time Complexity: O(h), where h is the height of the BST.

3.2 AVL Tree

An AVL tree defined as a self-balancing Binary Search Tree (BST) where the difference between heights of left and right subtrees for any node cannot be more than one. The difference between the heights of the left subtree and the right subtree for any node is known as the balance factor of the node. The AVL tree is named after its inventors, Georgy Adelson-Velsky and Evgenii Landis, who published it in their 1962 paper “An algorithm for the organization of information”.

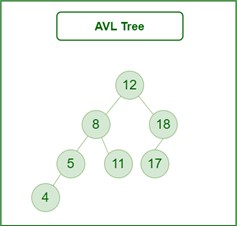
The above tree is AVL because the differences between the heights of left and right subtrees for every node are less than or equal to 1.

Insertion in an AVL Tree

AVL Tree: AVL tree is a self-balancing Binary Search Tree (BST) where the difference between heights of left and right subtrees cannot be more than one for all nodes.

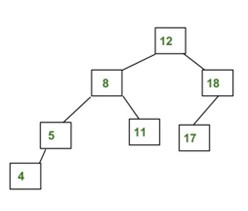
The above tree is AVL because the differences between the heights of left and right subtrees for every node are less than or equal to 1.

Deletion in an AVL Tree

To make sure that the given tree remains AVL after every deletion, we must augment the standard BST delete operation to perform some re-balancing. Following are two basic operations that can be performed to re-balance a BST without violating the BST property (keys(left) < key(root) < keys(right)).

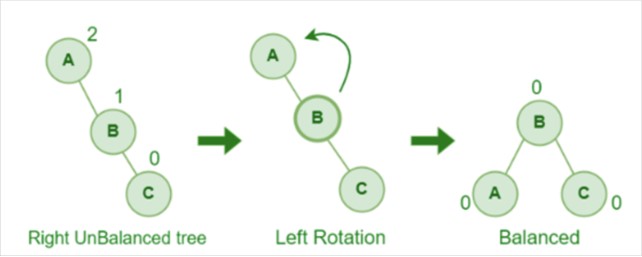
Left Rotation: When a node is added into the right subtree of the right subtree, if the tree gets out of balance, we do a single left rotation.

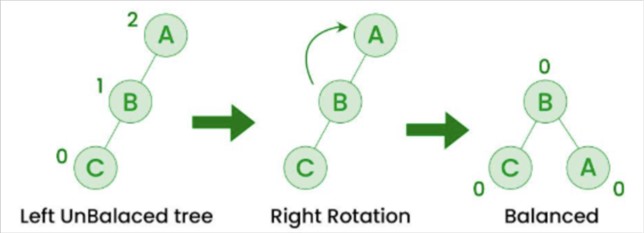
Right Rotation: If a node is added to the left subtree of the left subtree, the AVL tree may get out of balance, we do a single right rotation.

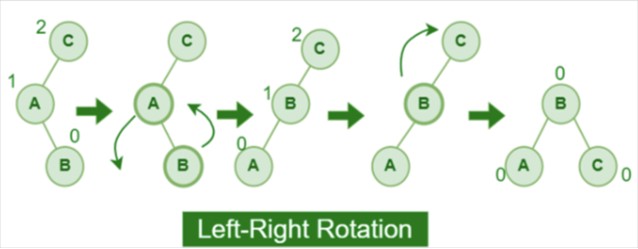
Left-Right Rotation: A left-right rotation is a combination in which first left rotation takes place after that right rotation executes.

Right-Left Rotation: A right-left rotation is a combination in which first right rotation takes place after that left rotation executes.

class Node:
    def __init__(self, key):
        self.key = key
        self.left = None
        self.right = None
        self.height = 1

def height(N):
    if N is None:
        return 0
    return N.height

def right_rotate(y):
    x = y.left
    T2 = x.right

# Perform rotation
    x.right = y
    y.left = T2

# Update heights
    y.height = max(height(y.left), 
                   height(y.right)) + 1
    x.height = max(height(x.left), 
                   height(x.right)) + 1

# Return new root
    return x

def left_rotate(x):
    y = x.right
    T2 = y.left

# Perform rotation
    y.left = x
    x.right = T2

# Update heights
    x.height = max(height(x.left), 
                   height(x.right)) + 1
    y.height = max(height(y.left), 
                   height(y.right)) + 1

# Return new root
    return y

def get_balance(N):
    if N is None:
        return 0
    return height(N.left) - height(N.right)

def insert(node, key):
    # 1. Perform the normal BST insertion
    if node is None:
        return Node(key)

if key < node.key:
        node.left = insert(node.left, key)
    elif key > node.key:
        node.right = insert(node.right, key)
    else:  # Duplicate keys not allowed
        return node

# 2. Update height of this ancestor node
    node.height = max(height(node.left), 
                      height(node.right)) + 1

# 3. Get the balance factor of this node
    # to check whether this node became 
    # unbalanced
    balance = get_balance(node)

# If this node becomes unbalanced, then
    # there are 4 cases

# Left Left Case
    if balance > 1 and key < node.left.key:
        return right_rotate(node)

# Right Right Case
    if balance < -1 and key > node.right.key:
        return left_rotate(node)

# Left Right Case
    if balance > 1 and key > node.left.key:
        node.left = left_rotate(node.left)
        return right_rotate(node)

# Right Left Case
    if balance < -1 and key < node.right.key:
        node.right = right_rotate(node.right)
        return left_rotate(node)

return node

def min_value_node(node):
    current = node

# loop down to find the leftmost leaf
    while current.left is not None:
        current = current.left

return current

def delete_node(root, key):
    # STEP 1: PERFORM STANDARD BST DELETE
    if root is None:
        return root

# If the key to be deleted is smaller 
    # than the root's key, then it lies in 
    # left subtree
    if key < root.key:
        root.left = delete_node(root.left, key)

# If the key to be deleted is greater 
    # than the root's key, then it lies in 
    # right subtree
    elif key > root.key:
        root.right = delete_node(root.right, key)

# if key is same as root's key, then 
    # this is the node to be deleted
    else:
        # node with only one child or no child
        if root.left is None or root.right is None:
            temp = root.left if root.left else root.right

# No child case
            if temp is None:
                root = None
            else:  # One child case
                root = temp

else:
            # node with two children: Get the 
            # inorder successor (smallest in 
            # the right subtree)
            temp = min_value_node(root.right)

# Copy the inorder successor's 
            # data to this node
            root.key = temp.key

# Delete the inorder successor
            root.right = delete_node(root.right, temp.key)

# If the tree had only one node then return
    if root is None:
        return root

# STEP 2: UPDATE HEIGHT OF THE CURRENT NODE
    root.height = max(height(root.left), 
                      height(root.right)) + 1

# STEP 3: GET THE BALANCE FACTOR OF THIS 
    # NODE (to check whether this node 
    # became unbalanced)
    balance = get_balance(root)

# If this node becomes unbalanced, then 
    # there are 4 cases

# Left Left Case
    if balance > 1 and get_balance(root.left) >= 0:
        return right_rotate(root)

# Left Right Case
    if balance > 1 and get_balance(root.left) < 0:
        root.left = left_rotate(root.left)
        return right_rotate(root)

# Right Right Case
    if balance < -1 and get_balance(root.right) <= 0:
        return left_rotate(root)

# Right Left Case
    if balance < -1 and get_balance(root.right) > 0:
        root.right = right_rotate(root.right)
        return left_rotate(root)

return root

def pre_order(root):
    if root is not None:
        print("{0} ".format(root.key), end="")
        pre_order(root.left)
        pre_order(root.right)

# Driver Code
if __name__ == "__main__":
    root = None

# Constructing tree given in the 
    # above figure
    root = insert(root, 9)
    root = insert(root, 5)
    root = insert(root, 10)
    root = insert(root, 0)
    root = insert(root, 6)
    root = insert(root, 11)
    root = insert(root, -1)
    root = insert(root, 1)
    root = insert(root, 2)

print("Preorder traversal of the "
          "constructed AVL tree is")
    pre_order(root)

root = delete_node(root, 10)

print("\nPreorder traversal after"
          " deletion of 10")
    pre_order(root)

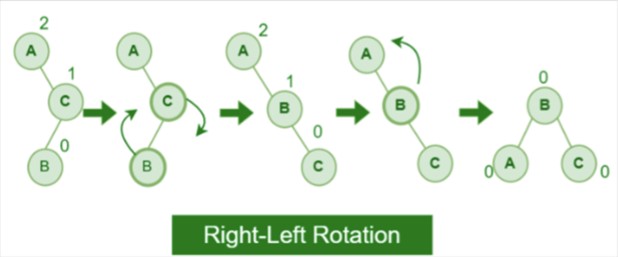
Insertion at AVL tree:

class Node:
    def __init__(self, key):
        self.key = key
        self.left = None
        self.right = None
        self.height = 1

# A utility function to get the 
# height of the tree
def height(node):
    if not node:
        return 0
    return node.height

# A utility function to right rotate 
# subtree rooted with y
def right_rotate(y):
    x = y.left
    T2 = x.right

# Perform rotation
    x.right = y
    y.left = T2

# Update heights
    y.height = 1 + max(height(y.left), height(y.right))
    x.height = 1 + max(height(x.left), height(x.right))

# Return new root
    return x

# A utility function to left rotate 
# subtree rooted with x
def left_rotate(x):
    y = x.right
    T2 = y.left

# Perform rotation
    y.left = x
    x.right = T2

# Update heights
    x.height = 1 + max(height(x.left), height(x.right))
    y.height = 1 + max(height(y.left), height(y.right))

# Return new root
    return y

# Get balance factor of node N
def get_balance(node):
    if not node:
        return 0
    return height(node.left) - height(node.right)

# Recursive function to insert a key in
# the subtree rooted with node
def insert(node, key):
  
    # Perform the normal BST insertion
    if not node:
        return Node(key)

if key < node.key:
        node.left = insert(node.left, key)
    elif key > node.key:
        node.right = insert(node.right, key)
    else:
        # Equal keys are not allowed in BST
        return node

# Update height of this ancestor node
    node.height = 1 + max(height(node.left), height(node.right))

# Get the balance factor of this ancestor node
    balance = get_balance(node)

# If this node becomes unbalanced, 
    # then there are 4 cases

# Left Left Case
    if balance > 1 and key < node.left.key:
        return right_rotate(node)

# Right Right Case
    if balance < -1 and key > node.right.key:
        return left_rotate(node)

# Left Right Case
    if balance > 1 and key > node.left.key:
        node.left = left_rotate(node.left)
        return right_rotate(node)

# Right Left Case
    if balance < -1 and key < node.right.key:
        node.right = right_rotate(node.right)
        return left_rotate(node)

# Return the (unchanged) node pointer
    return node

# A utility function to print preorder 
# traversal of the tree
def pre_order(root):
    if root:
        print(root.key, end=" ")
        pre_order(root.left)
        pre_order(root.right)

# Driver code
root = None

# Constructing tree given in the above figure
root = insert(root, 10)
root = insert(root, 20)
root = insert(root, 30)
root = insert(root, 40)
root = insert(root, 50)
root = insert(root, 25)

# The constructed AVL Tree would be
#        30
#       /  \
#      20   40
#     /  \    \
#    10  25   50

print("Preorder traversal :")
pre_order(root)

Output:

Preorder traversal :30 20 10 25 40 50

Time Complexity: O(log(n)), For Insertion

Deletion at AVL tree: