School of Computing - Learning Python

Module 23. Graphs (Graph Theory)

Learning Objectives

Understand the fundamental principles of graph modeling, implementation, and practical applications using Python libraries.
Define the key terms; participants should recognize that a graph comprises nodes (or vertices) connected by edges, forming structures that can represent various real-world scenarios.
Explain the different types of graphs such as directed, undirected, and weighted graphs is crucial for understanding how to model various relationships.
Implement graphs in Python effectively. Python does not have a built-in graph data type, so student need to familiarize themselves with alternative representations, such as using dictionaries or custom classes. This includes creating, modifying, and accessing graph structures through practical coding exercises, which strengthens programming skills alongside theoretical knowledge.

1. Introduction

A "graph" in mathematics and computer science consists of "nodes", also known as "vertices". Nodes may or may not be connected with one another. In our illustration, Figure 1, - which is a pictorial representation of a graph,

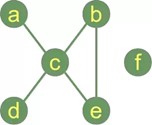
Figure 1. Graphs and its components.

The node "a" is connected with the node "c", but "a" is not connected with "b". The connecting line between two nodes is called an edge. If the edges between the nodes are undirected, the graph is called an undirected graph. If an edge is directed from one vertex (node) to another, a graph is called a directed graph. An directed edge is called an arc. Though graphs may look very theoretical, many practical problems can be represented by graphs. They are often used to model problems or situations in physics, biology, psychology and above all in computer science. In computer science, graphs are used to represent networks of communication, data organization, computational devices, the flow of computation, In the latter case, the are used to represent the data organization, like the file system of an operating system, or communication networks. The link structure of websites can be seen as a graph as well, i.e. a directed graph, because a link is a directed edge or an arc. Python has no built-in data type or class for graphs, but it is easy to implement them in Python. One data type is ideal for representing graphs in Python, i.e. dictionaries. The graph in our illustration can be implemented in the following way:

graph = { "a" : {"c"},
"b" : {"c", "e"},
"c" : {"a", "b", "d", "e"},
"d" : {"c"},
"e" : {"c", "b"},
"f" : {}
}

The keys of the dictionary above are the nodes of our graph. The corresponding values are sets with the nodes, which are connected by an edge. A set is better than a list or a tuple, because this way, we can have only one edge between two nodes. There is no simpler and more elegant way to represent a graph.

An edge can also be ideally implemented as a set with two elements, i.e. the end nodes. This is ideal for undirected graphs. For directed graphs we would prefer lists or tuples to implement edges.

Function to generate the list of all edges:

Output:

As we can see, there is no edge containing the node "f". "f" is an isolated node of our graph. The following Python function calculates the isolated nodes of a given graph:

Output:

2. Graphs as a Python Class

Before we go on with writing functions for graphs, we have a first go at a Python graph class implementation.

If you look at the following listing of our class, you can see in the init-method that we use a dictionary "self._graph_dict" for storing the vertices and their corresponding adjacent vertices.

""" A Python Class
A simple Python graph class, demonstrating the essential 
facts and functionalities of graphs.
"""

class Graph(object):

def __init__(self, graph_dict=None):
        """ initializes a graph object 
            If no dictionary or None is given, 
            an empty dictionary will be used
        """
        if graph_dict == None:
            graph_dict = {}
        self._graph_dict = graph_dict

def edges(self, vertice):
        """ returns a list of all the edges of a vertice"""
        return self._graph_dict[vertice]
        
    def all_vertices(self):
        """ returns the vertices of a graph as a set """
        return set(self._graph_dict.keys())

def all_edges(self):
        """ returns the edges of a graph """
        return self.__generate_edges()

def add_vertex(self, vertex):
        """ If the vertex "vertex" is not in 
            self._graph_dict, a key "vertex" with an empty
            list as a value is added to the dictionary. 
            Otherwise nothing has to be done. 
        """
        if vertex not in self._graph_dict:
            self._graph_dict[vertex] = []

def add_edge(self, edge):
        """ assumes that edge is of type set, tuple or list; 
            between two vertices can be multiple edges! 
        """
        edge = set(edge)
        vertex1, vertex2 = tuple(edge)
        for x, y in [(vertex1, vertex2), (vertex2, vertex1)]:
            if x in self._graph_dict:
                self._graph_dict[x].add(y)
            else:
                self._graph_dict[x] = [y]

def __generate_edges(self):
        """ A static method generating the edges of the 
            graph "graph". Edges are represented as sets 
            with one (a loop back to the vertex) or two 
            vertices 
        """
        edges = []
        for vertex in self._graph_dict:
            for neighbour in self._graph_dict[vertex]:
                if {neighbour, vertex} not in edges:
                    edges.append({vertex, neighbour})
        return edges
    
    def __iter__(self):
        self._iter_obj = iter(self._graph_dict)
        return self._iter_obj
    
    def __next__(self):
        """ allows us to iterate over the vertices """
        return next(self._iter_obj)

def __str__(self):
        res = "vertices: "
        for k in self._graph_dict:
            res += str(k) + " "
        res += "\nedges: "
        for edge in self.__generate_edges():
            res += str(edge) + " "
        return res
    
g = { "a" : {"d"},
      "b" : {"c"},
      "c" : {"b", "c", "d", "e"},
      "d" : {"a", "c"},
      "e" : {"c"},
      "f" : {}
    }

graph = Graph(g)

for vertice in graph:
    print(f"Edges of vertice {vertice}: ", graph.edges(vertice))

Output:

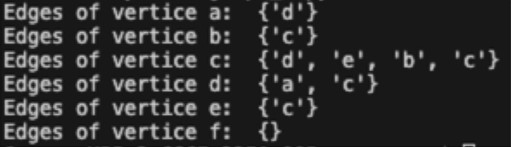
Let's calculate the list of all the vertices and the list of all the edges of our graph:

Output:

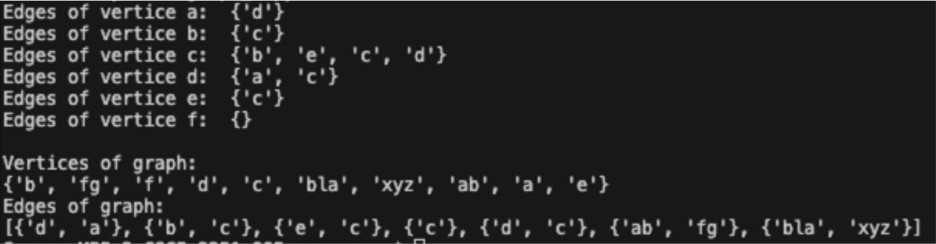
We add a vertex and and edge to the graph:

Output:

3. Paths in Graphs

Adjacent vertices:

Two vertices are adjacent when they are both incident to a common edge.

Path in an undirected Graph:

A path in an undirected graph is a sequence of vertices such that is adjacent to for 1 ≤ i < n. Such a path P is called a path of length n from to .

Simple Path:

A path with no repeated vertices is called a simple path.

Example:

(a, c, e) is a simple path in our graph, as well as (a,c,e,b). (a,c,e,b,c,d) is a path but not a simple path, because the node c appears twice.

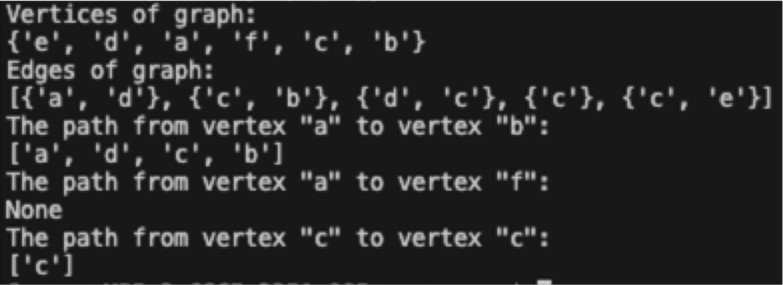
We add a method find_path to our class Graph. It tries to find a path from a start vertex to an end vertex. We also add a method find_all_paths, which finds all the paths from a start vertex to an end vertex:

""" A Python Class
A simple Python graph class, demonstrating the essential 
facts and functionalities of graphs.
"""

class Graph(object):

def all_edges(self):
        """ returns the edges of a graph """
        return self.__generate_edges()

def add_edge(self, edge):
        """ assumes that edge is of type set, tuple or list; 
            between two vertices can be multiple edges! 
        """
        edge = set(edge)
        vertex1, vertex2 = tuple(edge)
        for x, y in [(vertex1, vertex2), (vertex2, vertex1)]:
            if x in self._graph_dict:
                self._graph_dict[x].append(y)
            else:
                self._graph_dict[x] = [y]

def __str__(self):
        res = "vertices: "
        for k in self._graph_dict:
            res += str(k) + " "
        res += "\nedges: "
        for edge in self.__generate_edges():
            res += str(edge) + " "
        return res

def find_path(self, start_vertex, end_vertex, path=None):
        """ find a path from start_vertex to end_vertex 
            in graph """
        if path == None:
            path = []
        graph = self._graph_dict
        path = path + [start_vertex]
        if start_vertex == end_vertex:
            return path
        if start_vertex not in graph:
            return None
        for vertex in graph[start_vertex]:
            if vertex not in path:
                extended_path = self.find_path(vertex, 
                                               end_vertex, 
                                               path)
                if extended_path: 
                    return extended_path
        return None
    
    
    def find_all_paths(self, start_vertex, end_vertex, path=[]):
        """ find all paths from start_vertex to 
            end_vertex in graph """
        graph = self._graph_dict 
        path = path + [start_vertex]
        if start_vertex == end_vertex:
            return [path]
        if start_vertex not in graph:
            return []
        paths = []
        for vertex in graph[start_vertex]:
            if vertex not in path:
                extended_paths = self.find_all_paths(vertex, 
                                                     end_vertex, 
                                                     path)
                for p in extended_paths: 
                    paths.append(p)
        return paths

We check in the following the way of working of our find_path and find_all_paths methods.

4. Degree and Degree Sequence

The degree of a vertex is defined as the number of edges connected to it. The degree sequence of a graph is a list of vertex degrees sorted in non-increasing order. This information is crucial for many graph-theoretic algorithms, including those related to network connectivity and flow.

Graph Class: Contains methods to add vertices and edges and to compute the degrees.
add_vertex(vertex): Adds a new vertex to the graph if it does not already exist.
add_edge(vertex1, vertex2): Creates an undirected edge by adding both vertices to each other's adjacency list.
degree(vertex): Calculates the degree by returning the length of the adjacency list for the specified vertex.
degree_sequence(): Compiles the degree of all vertices, sorts them in non-increasing order, and returns the degree sequence.

class Graph:
    def __init__(self):
        """Initialize an empty graph."""
        self.graph_dict = {}
    
    def add_vertex(self, vertex):
        """Add a vertex to the graph."""
        if vertex not in self.graph_dict:
            self.graph_dict[vertex] = []

def add_edge(self, vertex1, vertex2):
        """Add an edge between two vertices."""
        if vertex1 not in self.graph_dict:
            self.add_vertex(vertex1)
        if vertex2 not in self.graph_dict:
            self.add_vertex(vertex2)
        
        self.graph_dict[vertex1].append(vertex2)
        self.graph_dict[vertex2].append(vertex1)  # For undirected graph
    
    def degree(self, vertex):
        """Return the degree of a vertex."""
        if vertex in self.graph_dict:
            return len(self.graph_dict[vertex])
        return 0
    
    def degree_sequence(self):
        """Return the degree sequence of the graph."""
        return sorted([self.degree(vertex) for vertex in self.graph_dict], reverse=True)

# Example usage
if __name__ == "__main__":
    g = Graph()
    g.add_edge("A", "B")
    g.add_edge("A", "C")
    g.add_edge("B", "C")
    g.add_edge("C", "D")
    
    print("Degree Sequence:", g.degree_sequence())

Output: show the degree sequence of the constructed graph based on the vertices and edges added.