Module 20. Sorting Algorithms

Learning Objectives

Understand the importance of sorting algorithms in organizing and arranging data efficiently.
Gain familiarity with various sorting techniques such as bubble sort, selection sort, insertion sort, merge sort, and quick sort.
Learn the implementation details of each sorting algorithm, including their time complexity.

1. Bubble Sort

Bubble sort, an algorithm for sorting, operates by comparing adjacent elements and swapping them until they are arranged correctly. A bubble sort makes several passes through the list. Following the first pass, the last element assumes the largest position in the list. Subsequently, after the second pass, the second-to-last element occupies the second-largest position. This iterative process persists until all elements are appropriately sorted.

1. How it works?

Let's say we have a list of elements, and we're attempting to sort the elements in ascending order.

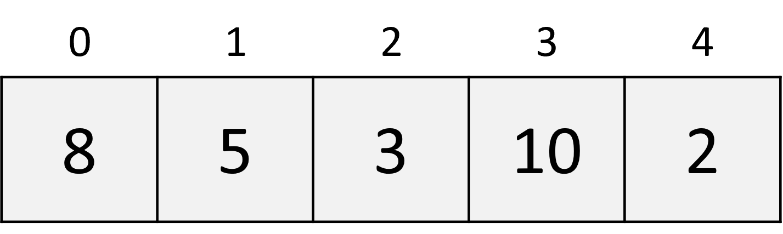
In bubble sort, two indices are utilized: one (i) for the pass and the other (j) for comparing adjacent elements during each pass.

a. 1^st pass (i = 0)

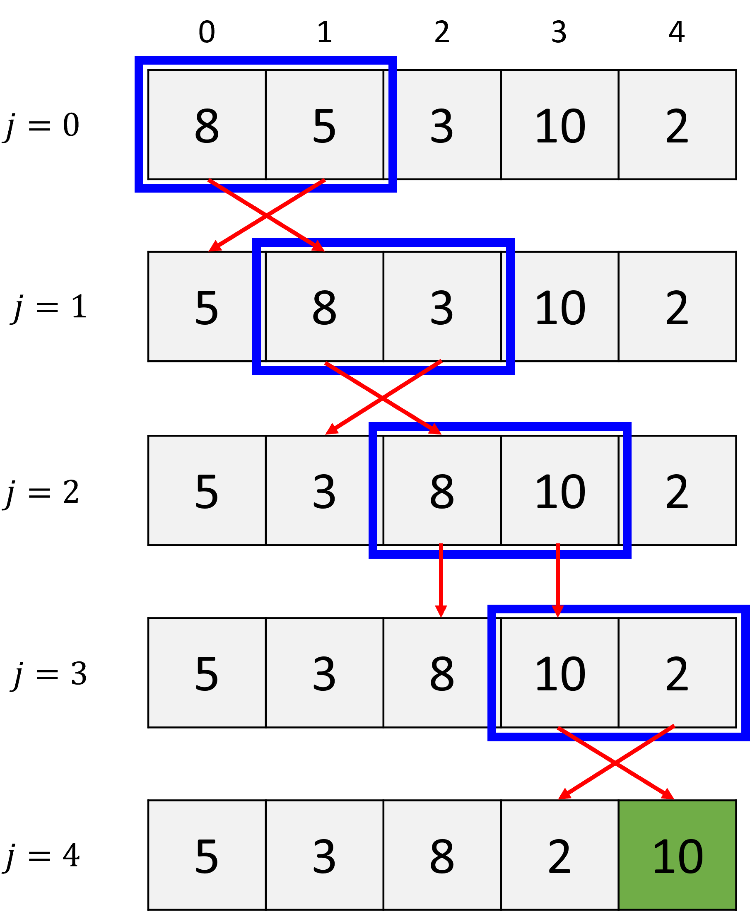
During the first pass (i = 0), the algorithm compares the first element (8) with the second element (5); since 8 is greater than 5, the two elements are swapped. Next, it compares the second element (8) with the third element (3); again, 8 is greater than 3, so they are swapped. Then, it compares the third element (8) with the fourth element (10), but no swap occurs in this case. Finally, it compares the fourth element (10) with the fifth element (2), resulting in a swap. Following the first pass, the bubble-sort algorithm ensures that the greatest element (10) is positioned at the last index of the list.

b. 2^nd pass (i = 1)

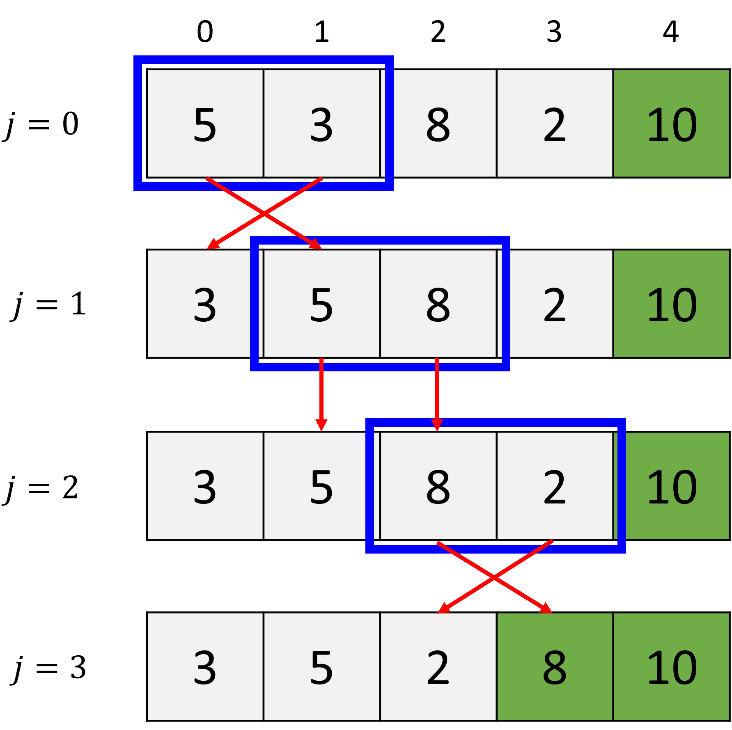
During the second pass (i = 1), the algorithm compares the first element (5) with the second element (3); as 5 is greater than 3, they are swapped. Next, it compares the second element (5) with the third element (8), resulting in no swap. Finally, it compares the third element (8) with the fourth element (2); since 8 is greater than 2, they are swapped. Consequently, after the second pass, the algorithm ensures that the second greatest element (8) is positioned as the second largest in the list.

c. 3^rd pass (i = 2)

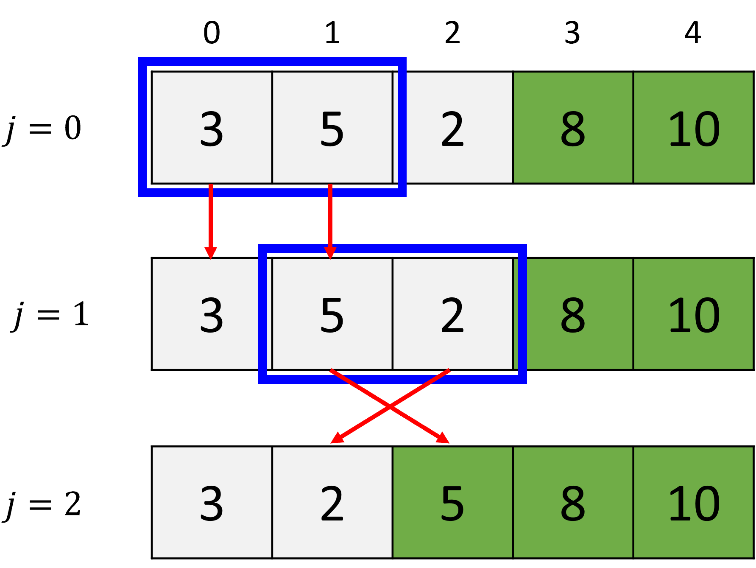
During the third pass (i = 2), the algorithm compares the first element (3) with the second element (5), resulting in no swap. Next, it compares the second element (5) with the third element (2); since 5 is greater than 2, they are swapped. As a result, after the third pass, the algorithm ensures that the third greatest element (5) is correctly positioned as the third largest in the list.

d. 4^th pass (i = 3)

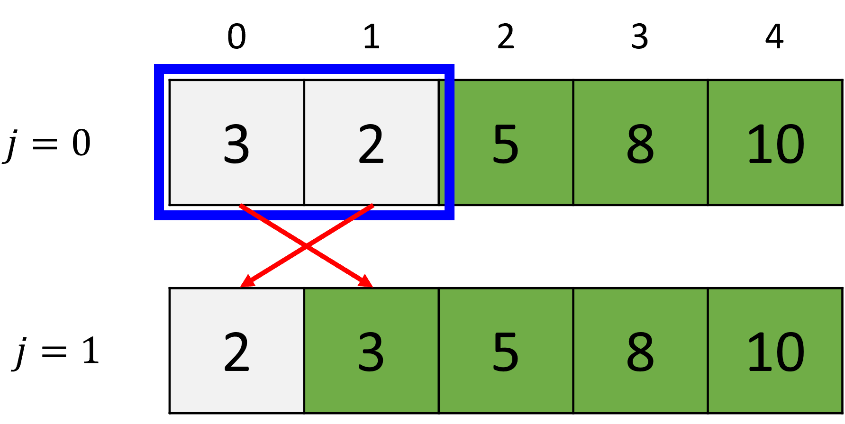
During the fourth pass (i = 3), the algorithm compares the first element (3) with the second element (2); as 3 is greater than 2, they are swapped. Consequently, after the fourth pass, the algorithm ensures that the fourth greatest element (3) is correctly positioned as the fourth largest in the list.

Finally, all elements are sorted in ascending order.

2. Bubble Sort Implementation

Example 1: Search for a number

Output:

[2, 3, 5, 8, 10]

Example 2: Search for a string

Output:

['Davis', 'John', 'Joshua', 'Lee', 'Tom']

3. Time Complexity

In the bubble sort algorithm, during each pass, the number of comparisons decreases by one. Specifically, in the first pass, there are n - 1 comparisons, in the second pass, n - 2 comparisons, and so on until the last pass with just one comparison. Summing these up, we get

Thus, the complexity of the bubble sort algorithm is O(n²).

2. Selection Sort

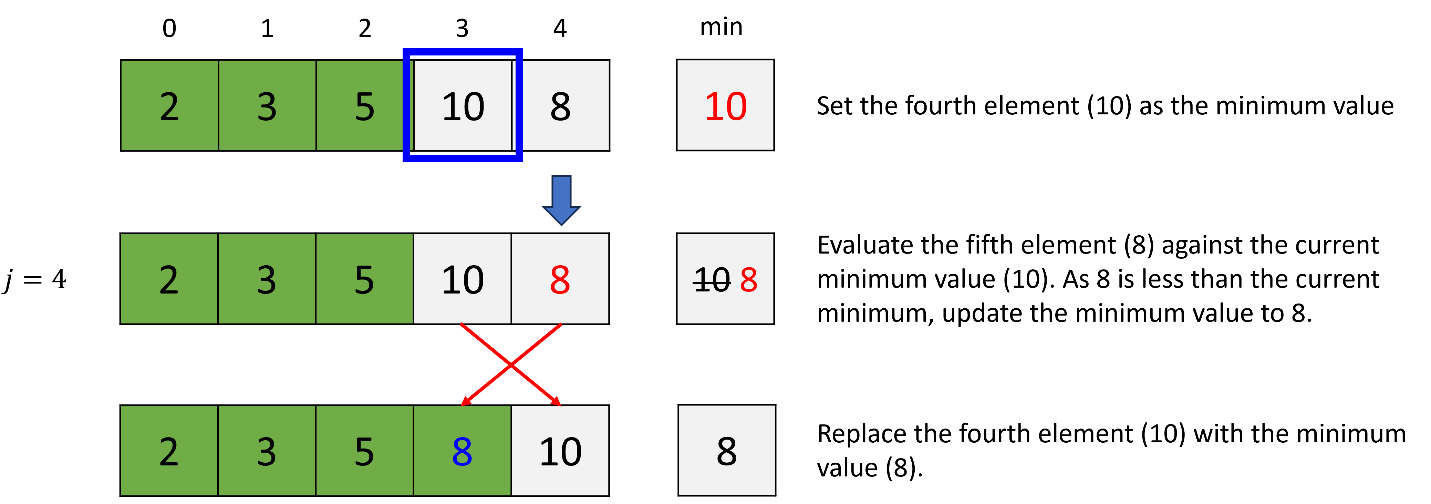
The selection sort algorithm locates the smallest number within the list and exchanges it with the first element. Subsequently, it identifies the smallest number among the remaining elements and swaps it with the second element, repeating this process until only one number remains.

1. How it works?

Let's say we have a list of elements, and we're attempting to sort the elements in ascending order.

In selection sort, two indices are utilized: one (i) for the iteration and the other (j) for finding the minimum element during each iteration.

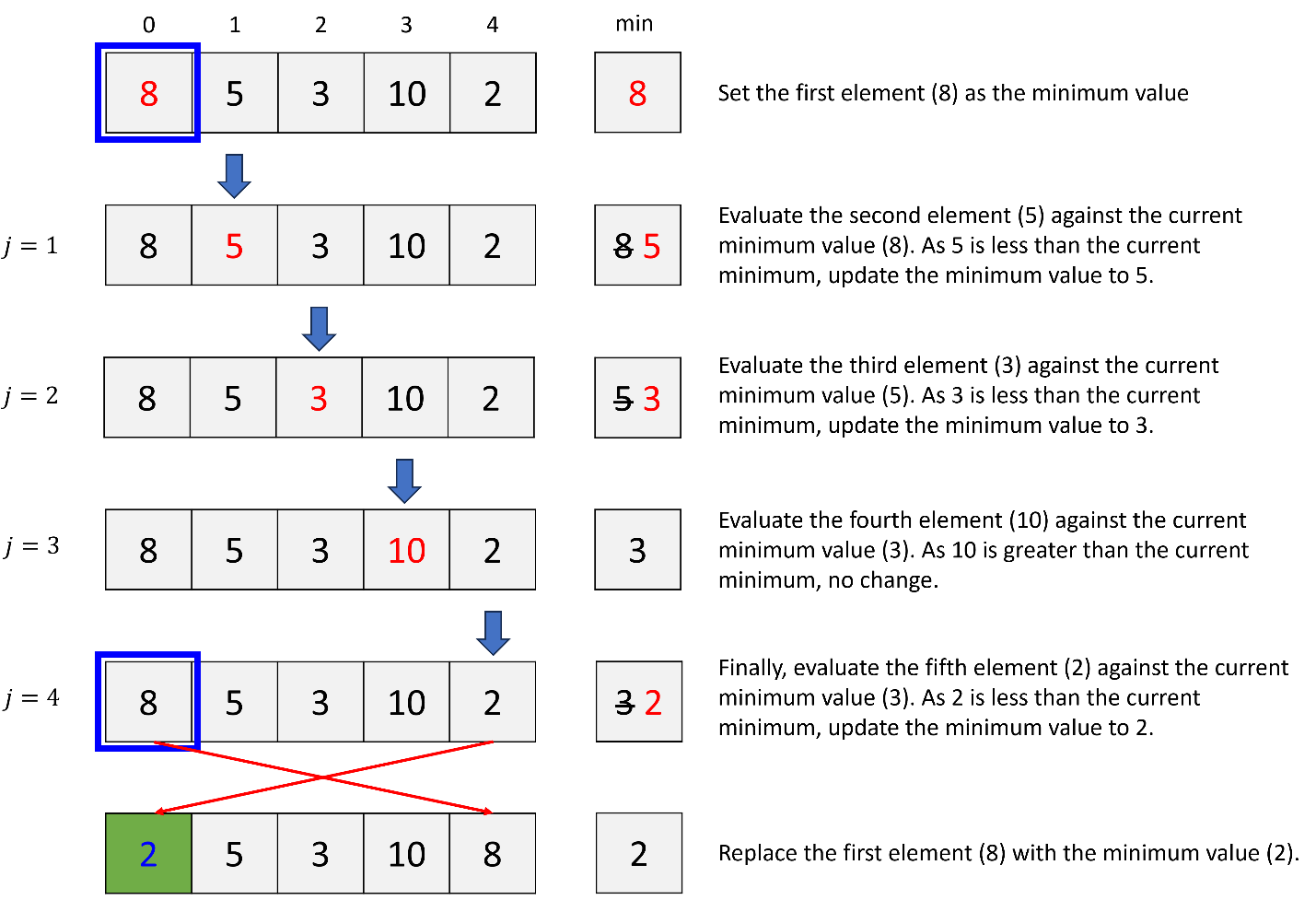
a. 1^st iteration (i = 0)

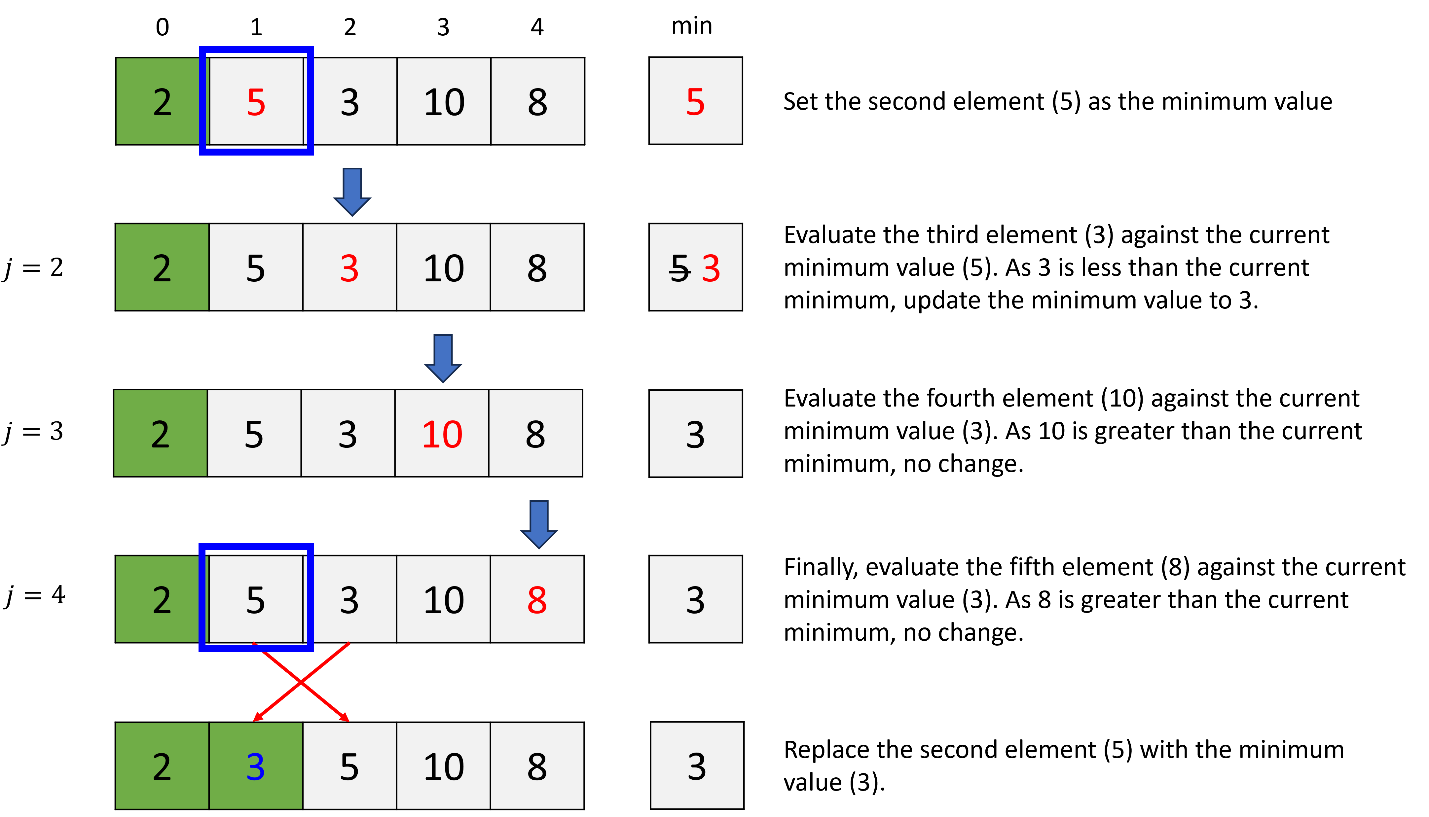
b. 2^nd iteration (i = 1)

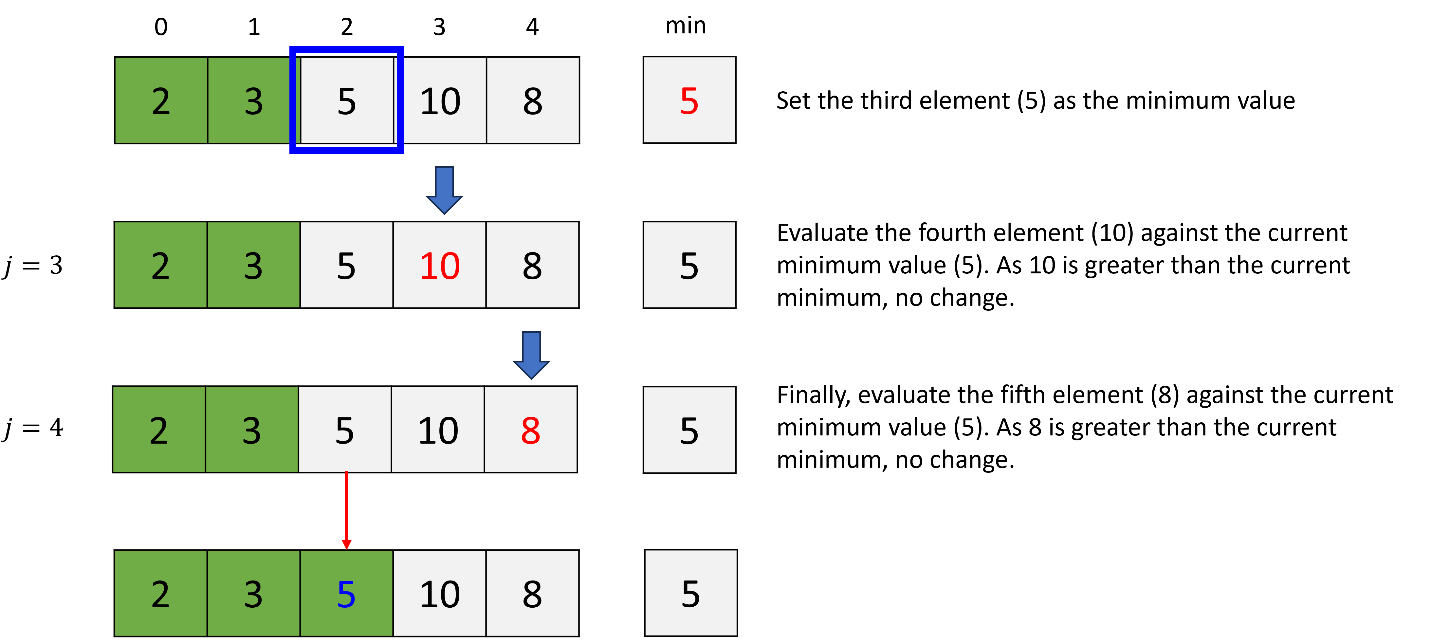
c. 3^rd iteration (i = 2)

d. 4^th iteration (i = 3)

2. Selection Sort Implementation

Output:

[2, 3, 5, 8, 10]

3. Time Complexity

In the selection sort algorithm, during each iteration, the number of comparisons decreases by one. Specifically, in the first pass, there are n - 1 comparisons, in the second pass, n - 2 comparisons, and so on until the last pass with just one comparison. Summing these up, we get

Thus, the complexity of the selection sort algorithm is O(n²).

3. Insertion Sort

The insertion sort algorithm organizes a list of values by iteratively inserting a new element into a pre-existing sorted sub-list until the entire list is sorted.

1. How it works?

Let's say we have a list of elements, and we're attempting to sort the elements in ascending order.

In insertion sort, two indices are utilized: one (i) for the iteration and the other (j) for comparing a new element with a pre-sorted element.

a. 1^st iteration (i = 1)

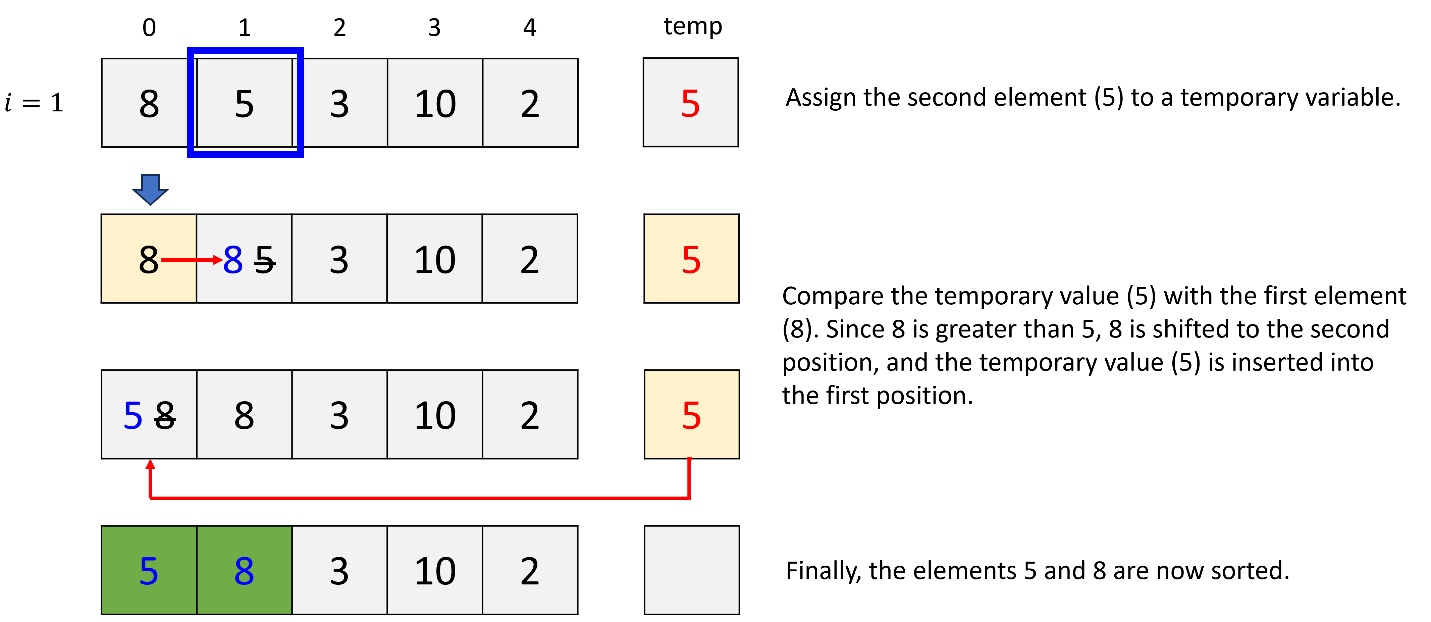
b. 2^nd iteration (i = 2)

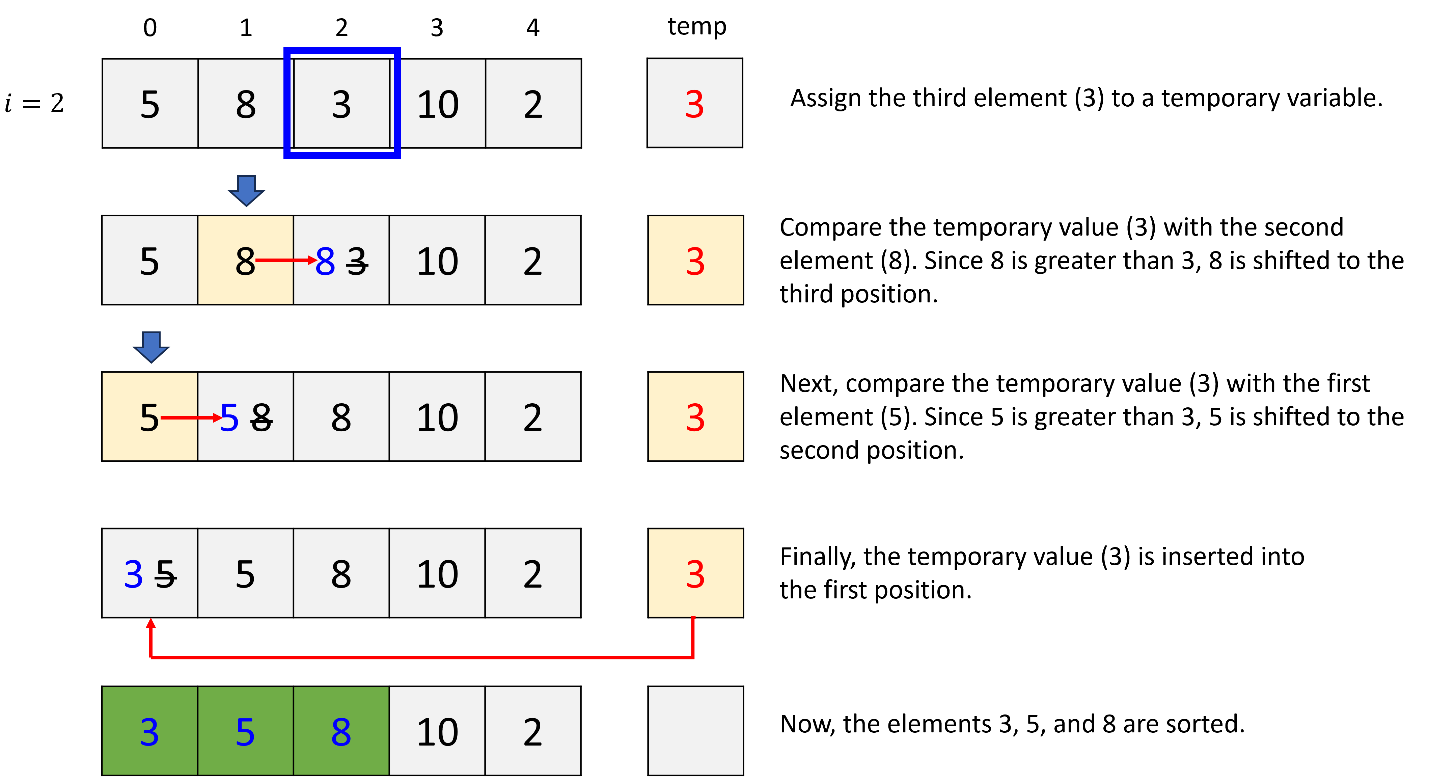
c. 3^rd iteration (i = 3)

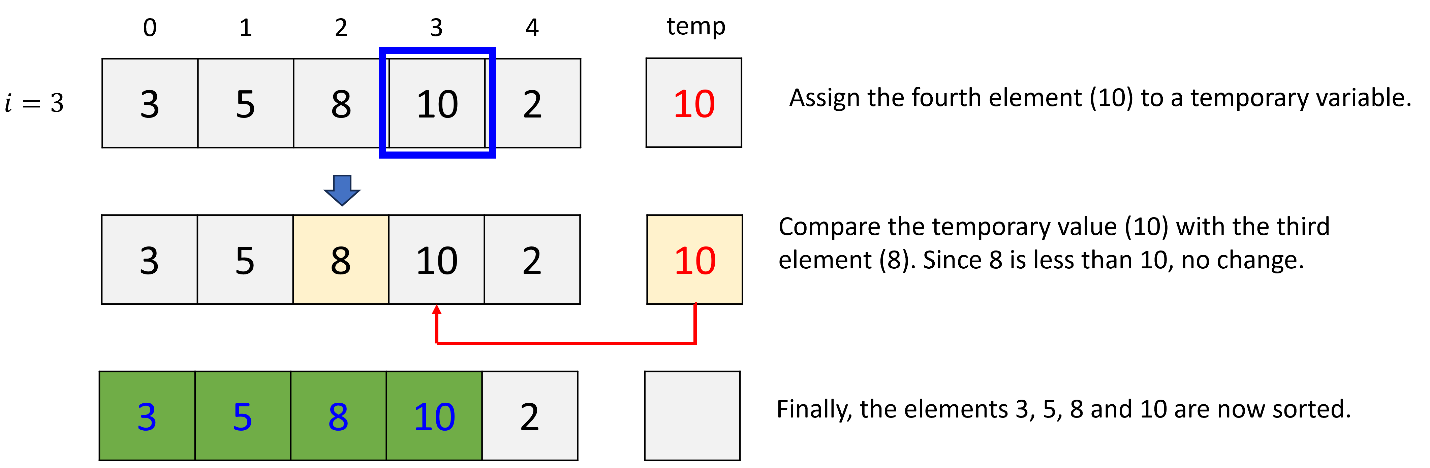
d. 4^th iteration (i = 4)

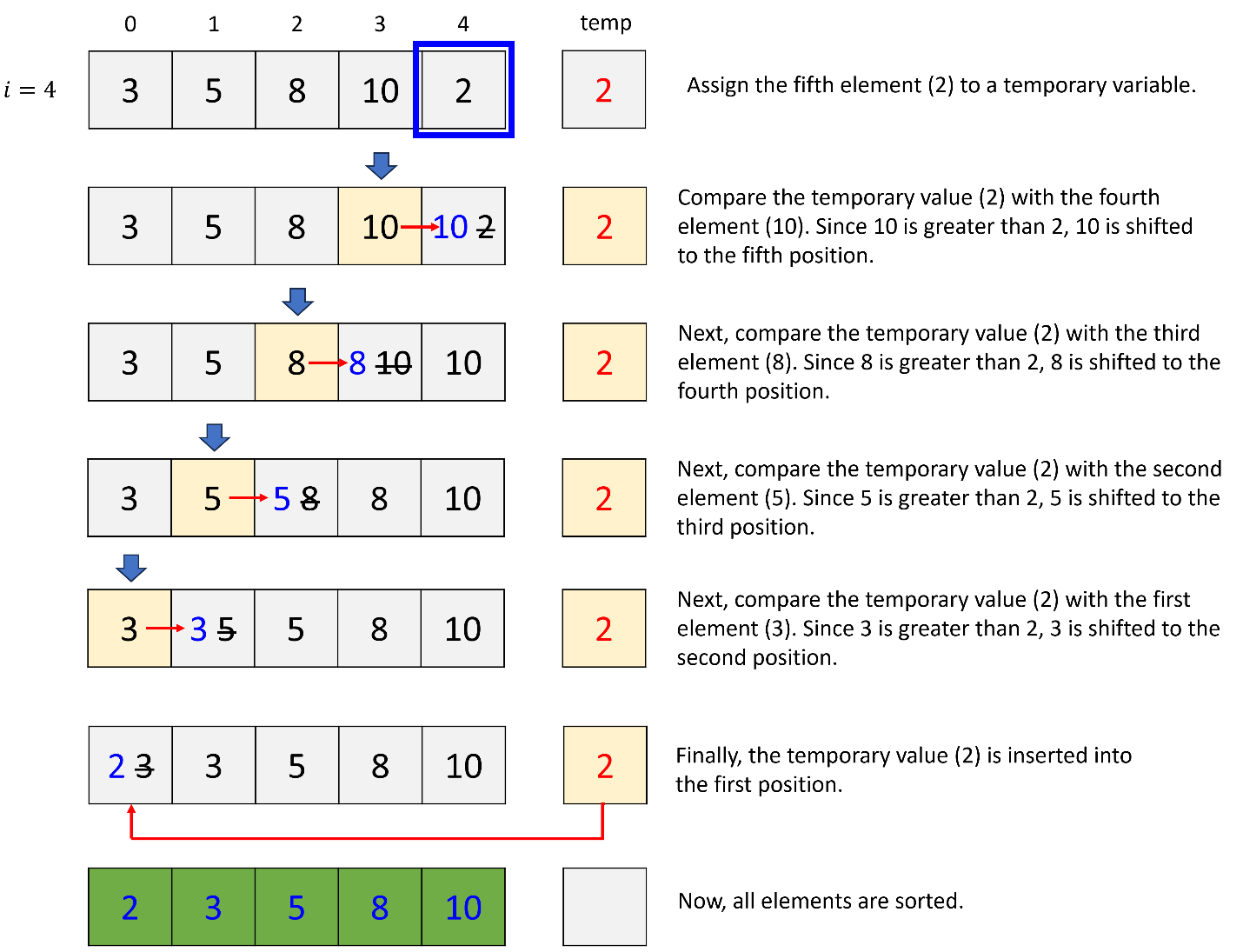
2. Insertion Sort Implementation

Output:

[2, 3, 5, 8, 10]

3. Time Complexity

In the worst-case scenario, where the list is initially in ascending order and requires sorting into descending order, the number of comparisons varies across each iteration. For the first iteration (i = 1), only 1 comparison is necessary, for the second iteration (i = 2), comparisons are needed, and so on until the (n - 1)th iteration. Summing these comparisons yields

Thus, the complexity of the selection sort algorithm in this scenario is O(n²).

Conversely, in the best-case scenario, where the list is already sorted in ascending order and requires sorting into ascending order again, only one comparison is needed per iteration. Hence, there are only n - 1 comparisons in total. Thus, the complexity of the selection sort algorithm in the best-case scenario is O(n).

4. Quick Sort

Quick sort is a sorting algorithm that utilizes the divide and conquer approach.

The quick sort algorithm operates in the following manner: it chooses a pivot element from the list. Then, it partitions the list into two segments, ensuring that all elements in the first segment are either less than or equal to the pivot, while all elements in the second segment are greater than the pivot. Apply the quick sort algorithm recursively to both the first and second segments.

1. How it works?

Let's say we have a list of elements, and we're attempting to sort the elements in ascending order.

a. Quick sort of all elements:

Firstly, apply the quick sort algorithm to all elements in the list.

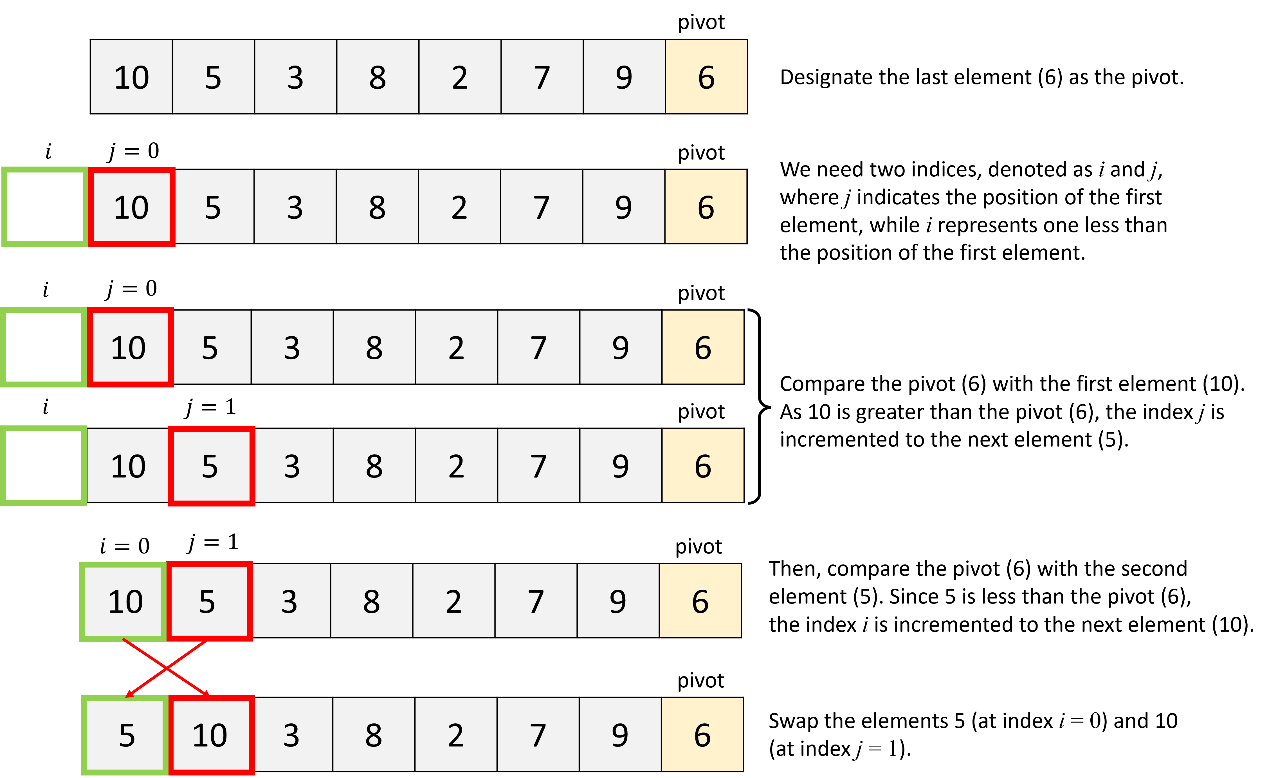
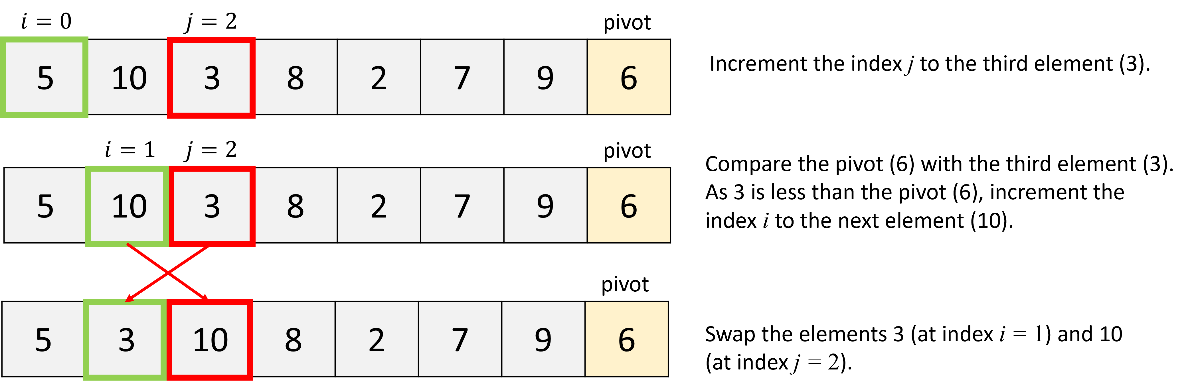
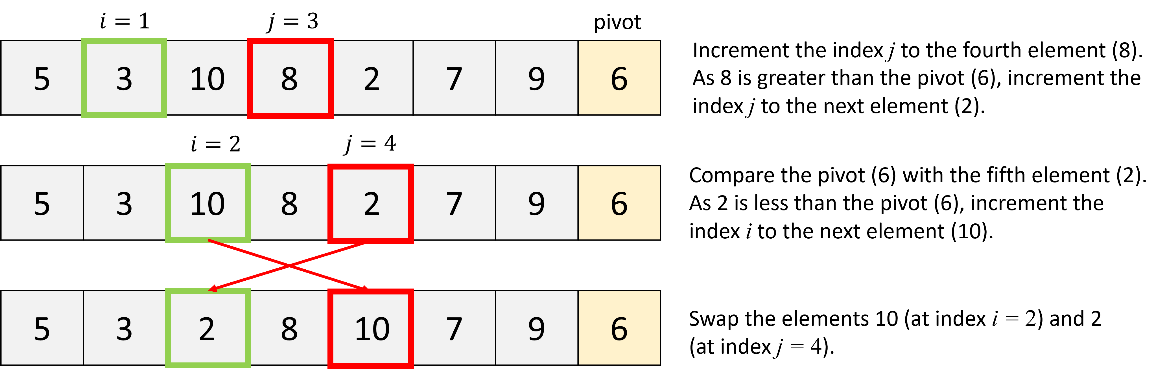
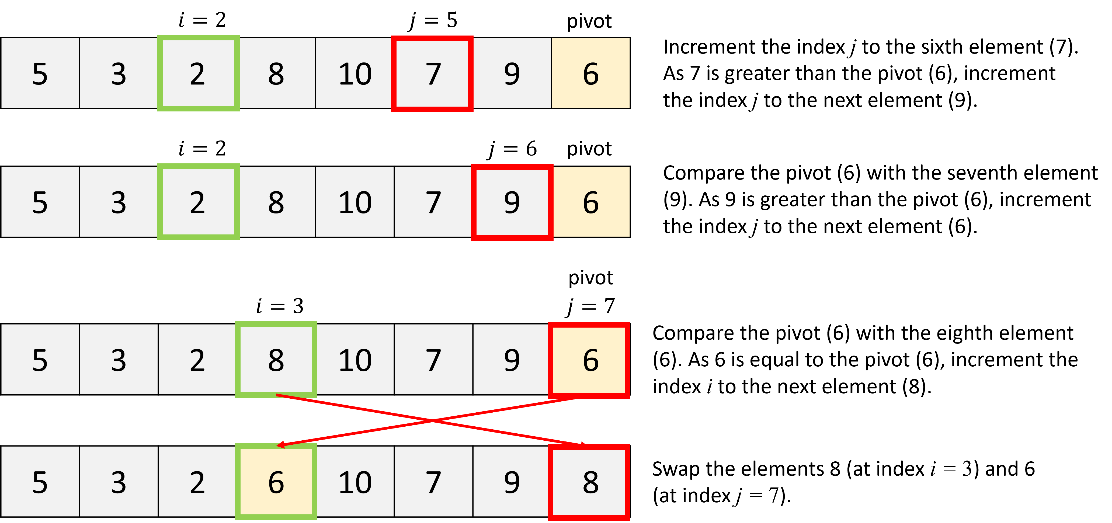
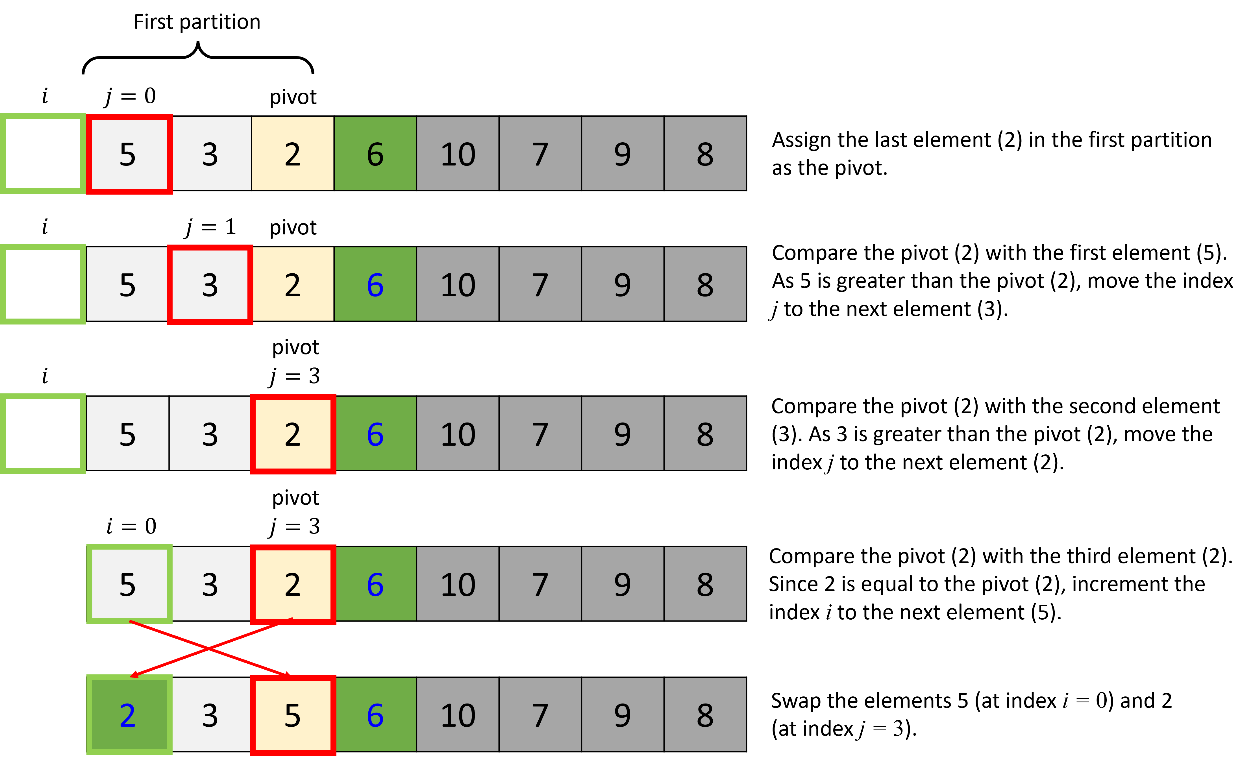
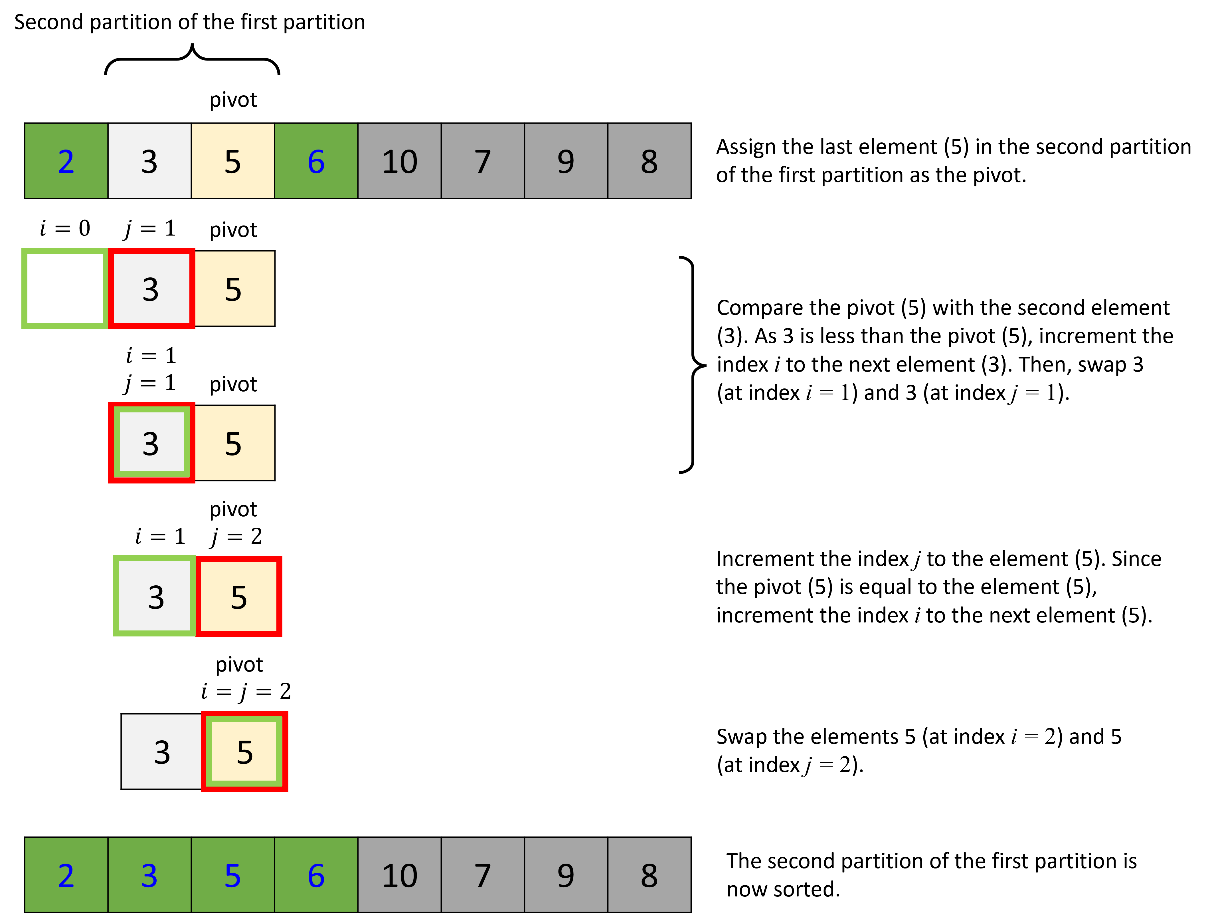
b. Quick sort of the first partition:

Next, apply the quick sort algorithm to the first partition in the list.

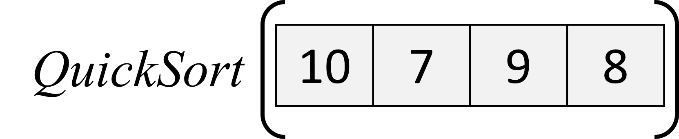
c. Quick sort of the second partition:

Next, apply the quick sort algorithm to the second partition in the list.

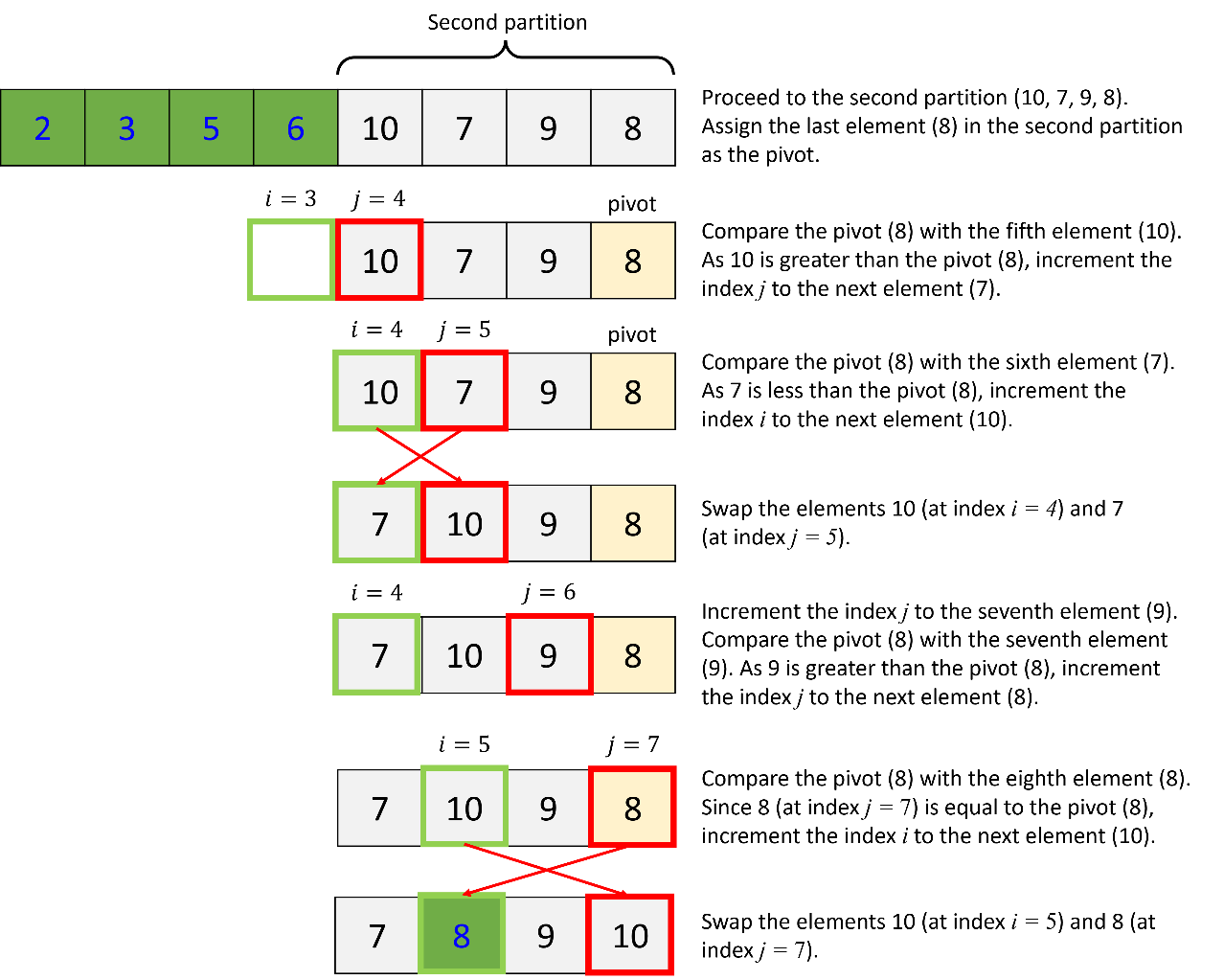
d. Quick sort of the first partition of the second partition:

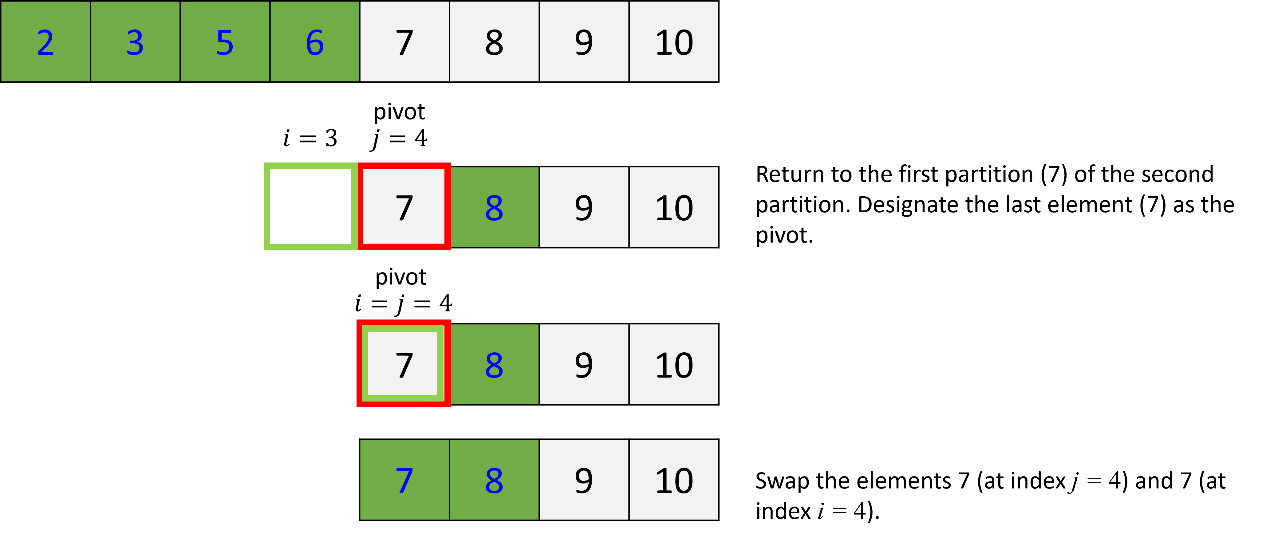
e. Quick sort of the second partition of the second partition:

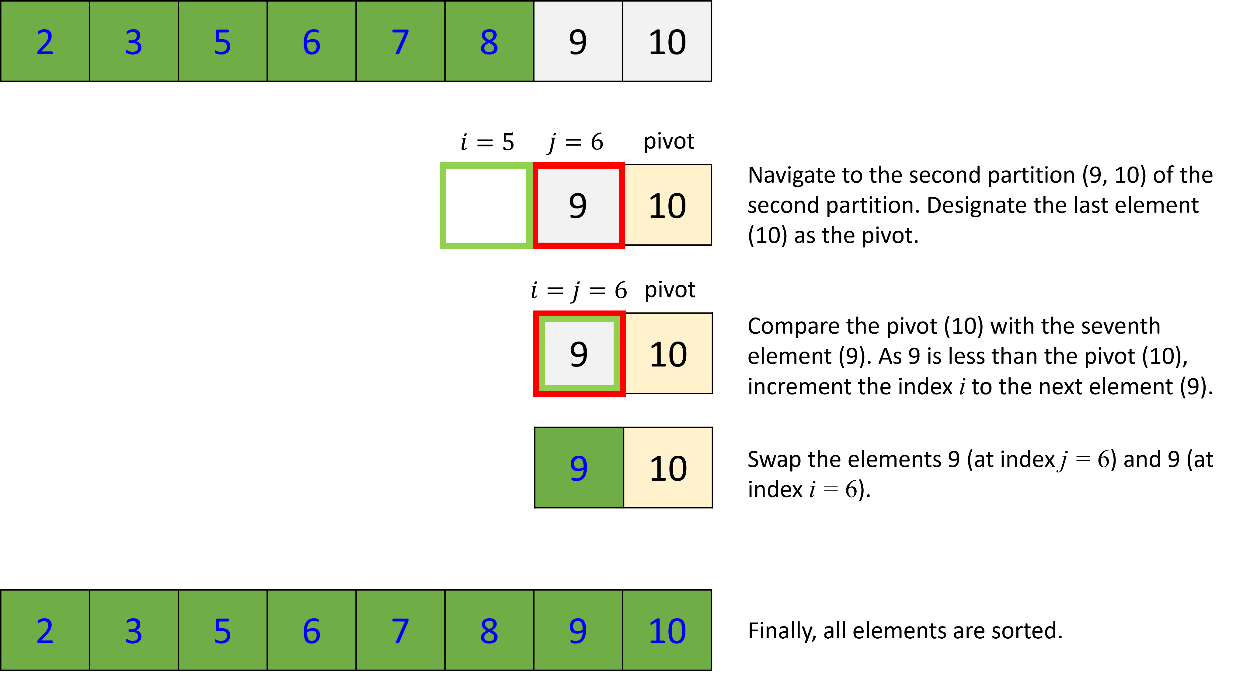
2. Quick Sort Implementation

# function to find the partition position
def partition(array, low, high):

# choose the rightmost element as pivot
    pivot = array[high]

# pointer for greater element
    i = low - 1

# traverse through all elements compare each element with pivot
    for j in range(low, high):
      if array[j] <= pivot:
        # if element smaller than pivot is found
        # swap it with the greater element pointed by i
        i = i + 1

# swapping element at i with element at j
        (array[i], array[j]) = (array[j], array[i])

# swap the pivot element with the greater element specified by i
    (array[i + 1], array[high]) = (array[high], array[i + 1])

# return the position from where partition is done
    return i + 1

# function to perform quicksort
def quickSort(array, low, high):
    if low < high:

# find pivot element such that
      # element smaller than pivot are on the left
      # element greater than pivot are on the right
      pi = partition(array, low, high)

# recursive call on the left of pivot
      quickSort(array, low, pi - 1)

# recursive call on the right of pivot
      quickSort(array, pi + 1, high)

def main():
    
    data = [10, 5, 3, 8, 2, 7, 9, 6]

size = len(data)

quickSort(data, 0, size - 1)

print('Sorted Array in Ascending Order:')
    print(data)

main()

Output:

[2, 3, 5, 6, 7, 8, 9, 10]

3. Time Complexity

In the worst-case scenario, each time the pivot is chosen, it divides the list into one large sublist and another empty sublist. The size of the larger sublist is one less than the size of the previous sublist. Thus, the complexity of the quick sort algorithm in this scenario is O(n²).

In the best case, each time the pivot is selected, it divides the array into two approximately equal-sized parts. Let T(n) denote the time required for sorting an array of elements using quicksort.

Hence,

The complexity is O(n log log n).

5. Merge Sort

The Merge sort algorithm operates recursively in the following manner: it divides the list into two halves and recursively applies merge sort to each half. Once both halves are sorted, the algorithm merges them together.

1. How it works?

Let's say we have a list of elements, and we're attempting to sort the elements in ascending order.

a. Divide a list into two sublists (left half and right half):

Initially, a list of elements (10, 5, 3, 8, 2, 7, 6) is divided into two sublists. The left sublist consists of (10, 5, 3, 8), while the right sublist comprises (2, 7, 9, 6).

b. Divide each sublist into two sublists, recursively:

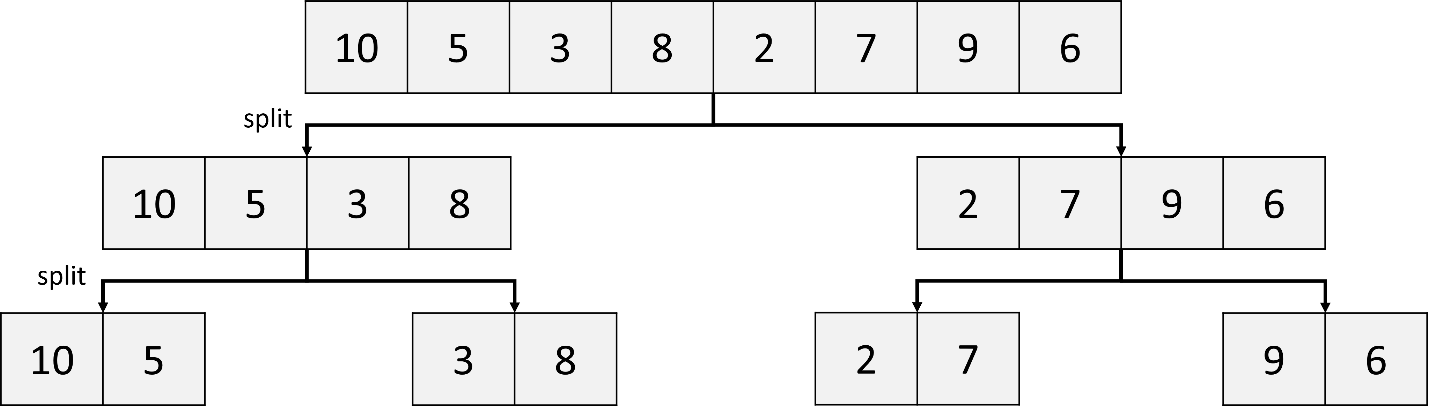
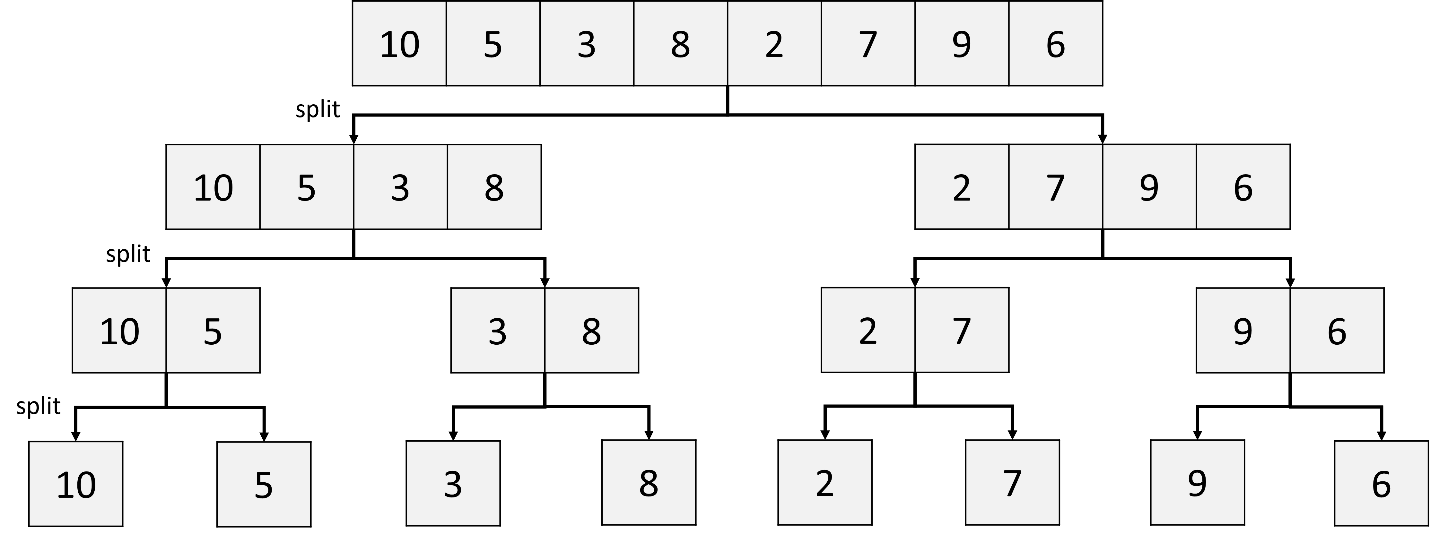
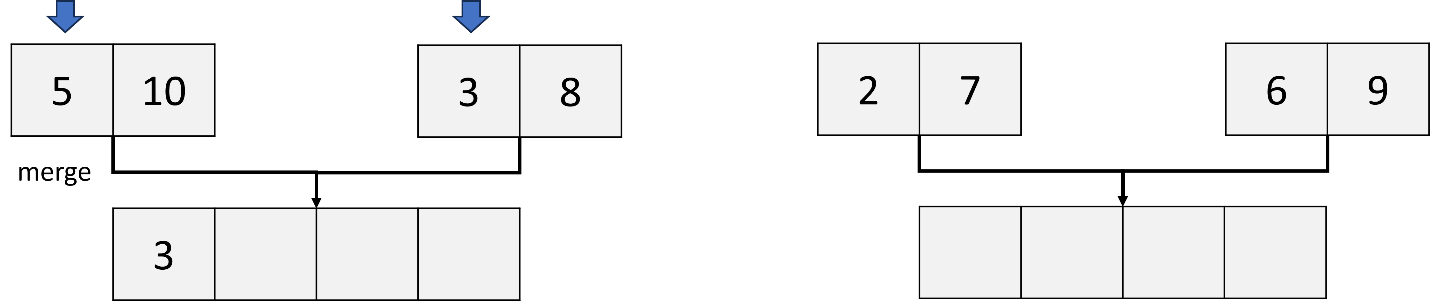
c. Merge two sublists: (10), (5); (3), (8); (2), (7); (9), (6)

Compare 10 and 5. Since 5 is less than 10, 5 is placed first in a new sorted list, followed by 10.
Compare 3 and 8. Since 3 is less than 8, 3 is placed first in a new sorted list, followed by 8.
Merge the sublists: (2, 7) and (6, 9).

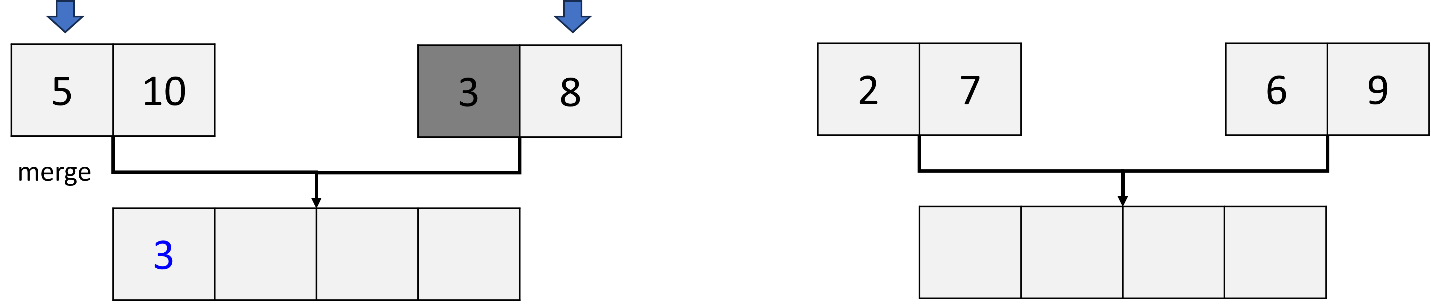
d. Merge two sublists, (5,10), (3,8); (2,7), (6,9):

Compare the first element (5) in the left sublist and the first element (3) in the right sublist. Since 3 is less than 5, 3 is placed first in a new sorted list.

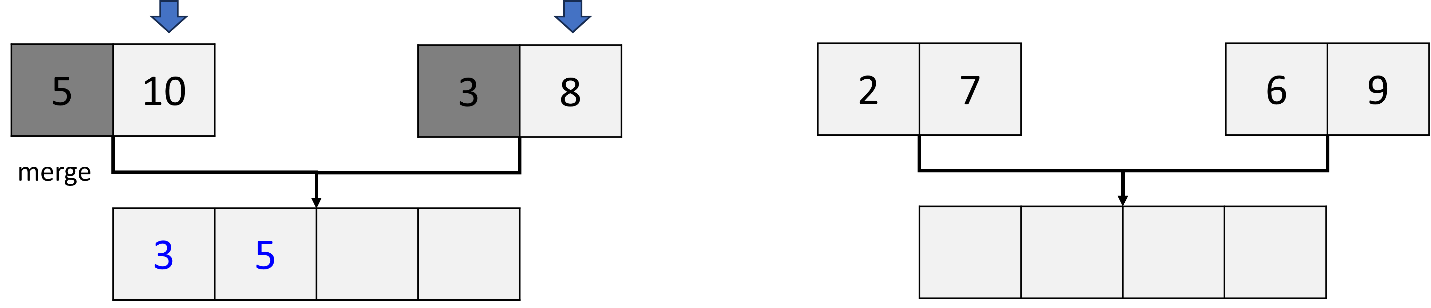
Move to the next element (8) in the right sublist. Compare the first element (5) in the left sublist with the second element (8) in the right sublist. Since 5 is less than 8, 5 is placed second in a new sorted list.

Move to the next element (10) in the left sublist. Compare the second element (10) in the left sublist with the second element (8) in the right sublist. Since 8 is less than 10, 8 is placed third in a new sorted list.

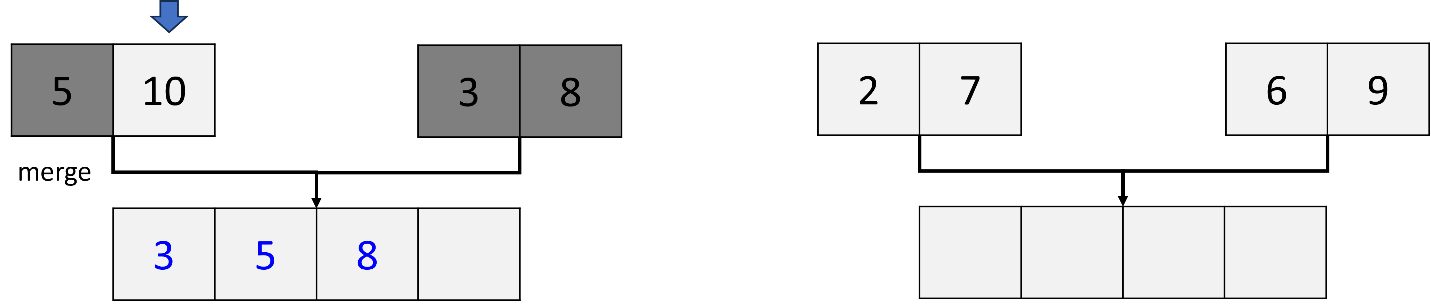
Finally, place the remaining element (10) from the left sublist into the last position in the new sorted list.

Similarly, the right sublists (2, 7) and (6, 9) are sorted as follows:

e. Merge two sublists, (3, 5,8, 10); (2, 6, 7, 9):

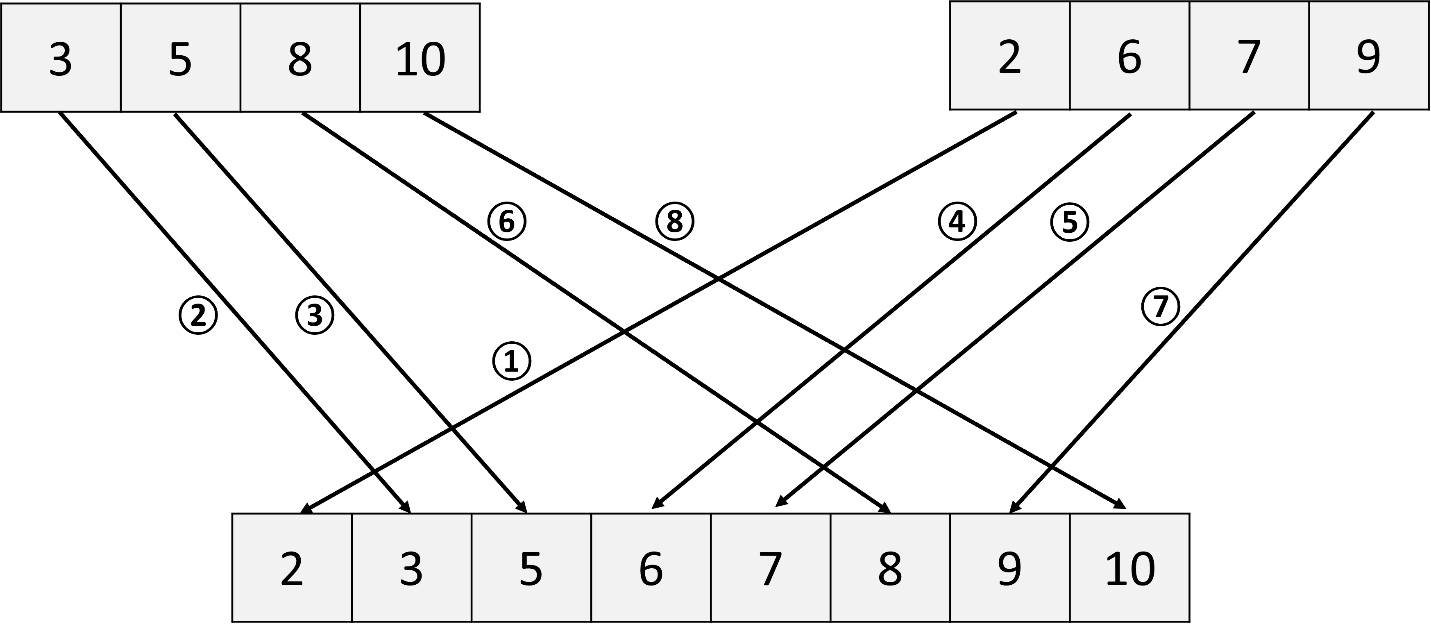
Similarly, compare elements in the sublist (3, 5, 8, 10) with the sublist (2, 6, 7, 9), and then place the smallest element into a new sorted list.

2. Merge Sort Implementation

def mergeSort(array):
    if len(array) > 1:

#  r is the point where the array is divided into two subarrays
        r = len(array)//2
        L = array[:r]
        M = array[r:]

# Sort the two halves
        mergeSort(L)
        mergeSort(M)

i = j = k = 0

# Until we reach either end of either L or M, pick larger among
        # elements L and M and place them in the correct position at  
          A[p..r]
        while i < len(L) and j < len(M):
            if L[i] < M[j]:
                array[k] = L[i]
                i += 1
            else:
                array[k] = M[j]
                j += 1
            k += 1

# When we run out of elements in either L or M,
        # pick up the remaining elements and put in A[p..r]
        while i < len(L):
            array[k] = L[i]
            i += 1
            k += 1

while j < len(M):
            array[k] = M[j]
            j += 1
            k += 1

# Print the array
def printList(array):
    for i in range(len(array)):
        print(array[i], end=" ")
    print()
    
def main():

data = [10, 5, 3, 8, 2, 7, 9, 6]

mergeSort(data)

print("Sorted array is: ")
    printList(data)

main()

Output:

2 3 5 6 7 8 9 10

3. Time Complexity

Let T(n) denote the time required for sorting an list of elements using merge sort. The merge sort algorithm divides the list into two sublists, sorts the sublists using the same algorithm recursively, and then merges the sublists. Therefore,

where represents the time for merging. Thus, the complexity is O(n log log n).

Summary

Bubble sort compares adjacent elements and swaps them if they are in the wrong order.
Bubble sort repeatedly passes through the list until no swaps are needed.
Time complexity of bubble sort is O(n²).
Selection sort divides the list into a sorted and an unsorted region.
Selection sort finds the smallest element in the unsorted region and swaps it with the leftmost unsorted element.
Time complexity of selection sort is O(n²).
Insertion sort builds a sorted list one element at a time by repeatedly inserting the next element into its proper position.
Time complexity of insertion sort is O(n²).
Merge sort divides the list into smaller sublists, sorts them recursively, and then merges them back together.
Time complexity of merge sort is O(n log log n).
Quick sort divides the list into two partitions based on a pivot element, then recursively sorts the partitions.
Time complexity of quick sort is O(n log log n) on average, but worst-case time complexity is O(n²).

Programming Exercises

Exercise 1: Sorting a List of Strings

Implement a Python script that sorts a list of strings in lexicographical order using any sorting algorithm. You can also explore sorting strings based on custom criteria, such as length or alphabetical order.

Exercise 2: Sorting a List of Custom Objects

Define a Python class representing custom objects and implement sorting functionality for lists of these objects. Use either the built-in sorting functions or implement sorting algorithms tailored to the specific properties of the custom objects.

Exercise 3: Top-K Elements

Write a Python function that takes a list of numbers and an integer k as input and returns the top-k elements from the list, sorted in descending order. You can use sorting algorithms like quick select to efficiently find the top-k elements.

Exercise 4: Sorting Dictionary by Values

Define a Python dictionary and write a function that sorts it based on the values in ascending or descending order. You can use any sorting algorithm or the built-in sorted() function with custom comparison functions.

Exercise 5: Sorting a List of Tuples

Implement a Python program that sorts a list of tuples based on specific elements within the tuples. You can customize the sorting criteria by providing key functions to the sorting algorithms.