Bubble sort, an algorithm for sorting, operates by comparing adjacent elements and swapping them until they are arranged correctly. A bubble sort makes several passes through the list. Following the first pass, the last element assumes the largest position in the list. Subsequently, after the second pass, the second-to-last element occupies the second-largest position. This iterative process persists until all elements are appropriately sorted.

1. How it works?

Let's say we have a list of elements, and we're attempting to sort the elements in ascending order.

In bubble sort, two indices are utilized: one (i) for the pass and the other (j) for comparing adjacent elements during each pass.

a. 1^st pass (i = 0)

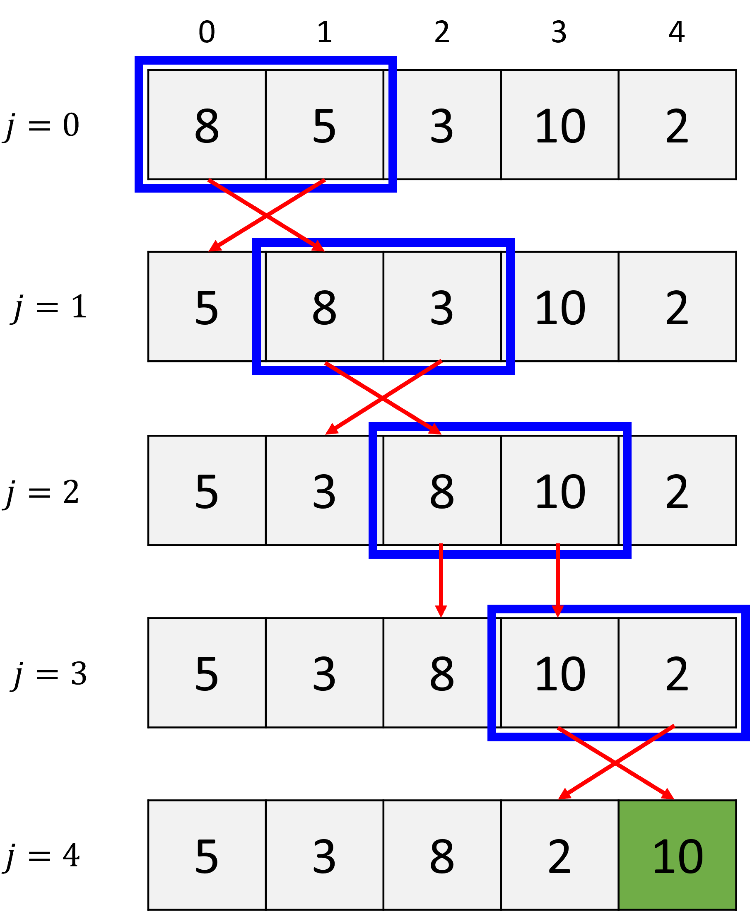
During the first pass (i = 0), the algorithm compares the first element (8) with the second element (5); since 8 is greater than 5, the two elements are swapped. Next, it compares the second element (8) with the third element (3); again, 8 is greater than 3, so they are swapped. Then, it compares the third element (8) with the fourth element (10), but no swap occurs in this case. Finally, it compares the fourth element (10) with the fifth element (2), resulting in a swap. Following the first pass, the bubble-sort algorithm ensures that the greatest element (10) is positioned at the last index of the list.

 

b. 2^nd pass (i = 1)

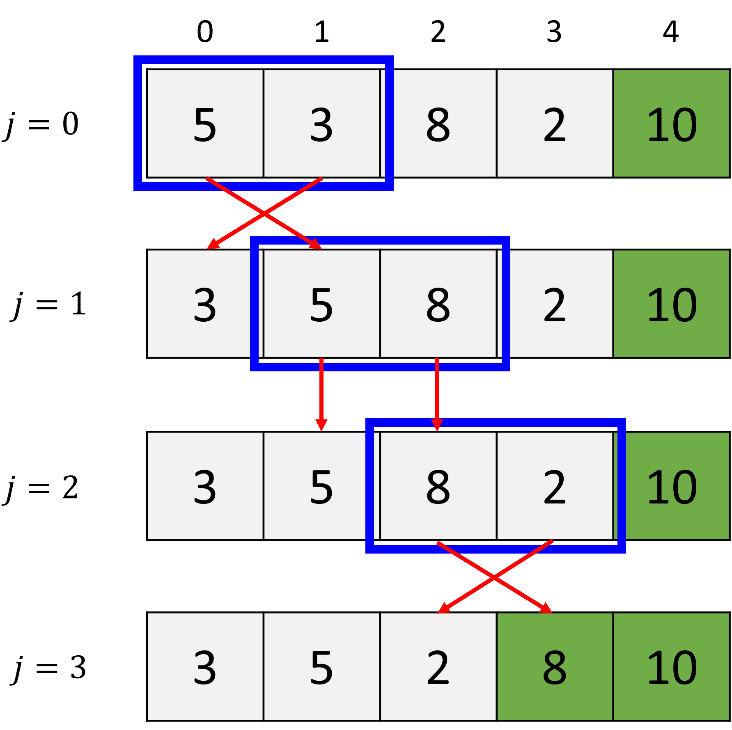
During the second pass (i = 1), the algorithm compares the first element (5) with the second element (3); as 5 is greater than 3, they are swapped. Next, it compares the second element (5) with the third element (8), resulting in no swap. Finally, it compares the third element (8) with the fourth element (2); since 8 is greater than 2, they are swapped. Consequently, after the second pass, the algorithm ensures that the second greatest element (8) is positioned as the second largest in the list.

 

c. 3^rd pass (i = 2)

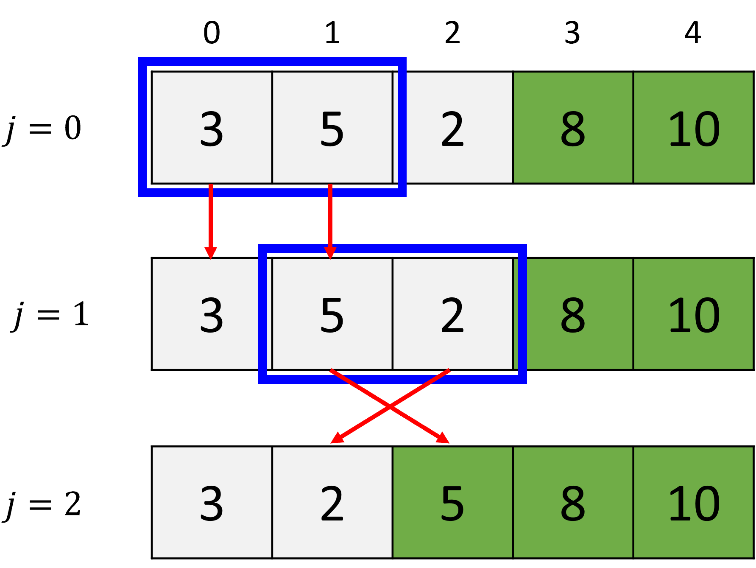
During the third pass (i = 2), the algorithm compares the first element (3) with the second element (5), resulting in no swap. Next, it compares the second element (5) with the third element (2); since 5 is greater than 2, they are swapped. As a result, after the third pass, the algorithm ensures that the third greatest element (5) is correctly positioned as the third largest in the list.

 

d. 4^th pass (i = 3)

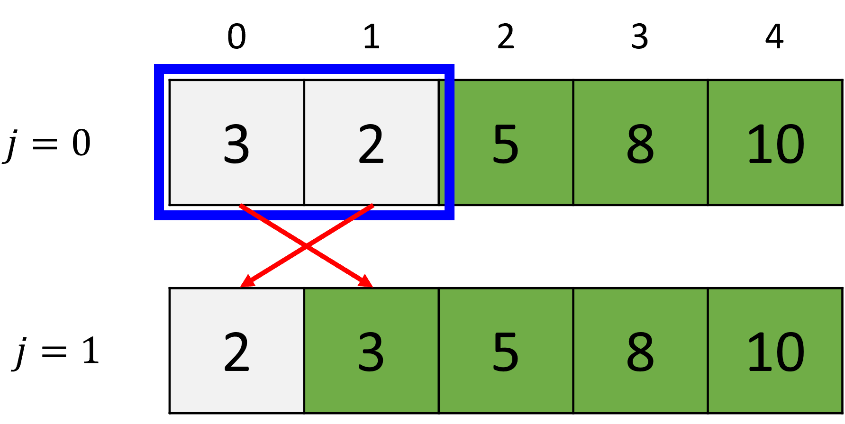
During the fourth pass (i = 3), the algorithm compares the first element (3) with the second element (2); as 3 is greater than 2, they are swapped. Consequently, after the fourth pass, the algorithm ensures that the fourth greatest element (3) is correctly positioned as the fourth largest in the list.

Finally, all elements are sorted in ascending order.

 

2. Bubble Sort Implementation

Example 1: Search for a number

 

Output:

[2, 3, 5, 8, 10]

 

Example 2: Search for a string

 

Output:

['Davis', 'John', 'Joshua', 'Lee', 'Tom']

 

3. Time Complexity

In the bubble sort algorithm, during each pass, the number of comparisons decreases by one. Specifically, in the first pass, there are n - 1 comparisons, in the second pass, n - 2 comparisons, and so on until the last pass with just one comparison. Summing these up, we get

Thus, the complexity of the bubble sort algorithm is O(n²).