The insertion sort algorithm organizes a list of values by iteratively inserting a new element into a pre-existing sorted sub-list until the entire list is sorted.

1. How it works?

Let's say we have a list of elements, and we're attempting to sort the elements in ascending order.

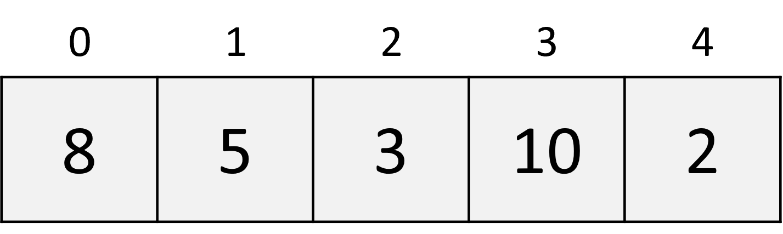
In insertion sort, two indices are utilized: one (i) for the iteration and the other (j) for comparing a new element with a pre-sorted element.

 

a. 1^st iteration (i = 1)

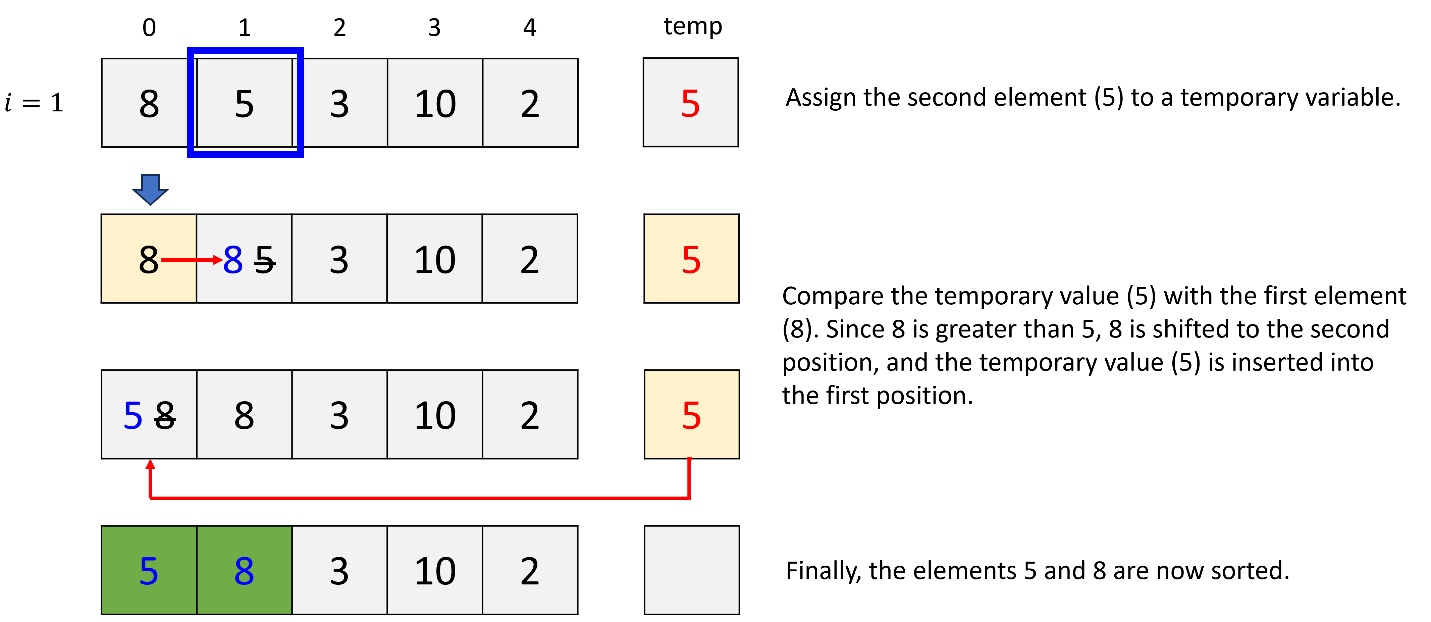
b. 2^nd iteration (i = 2)

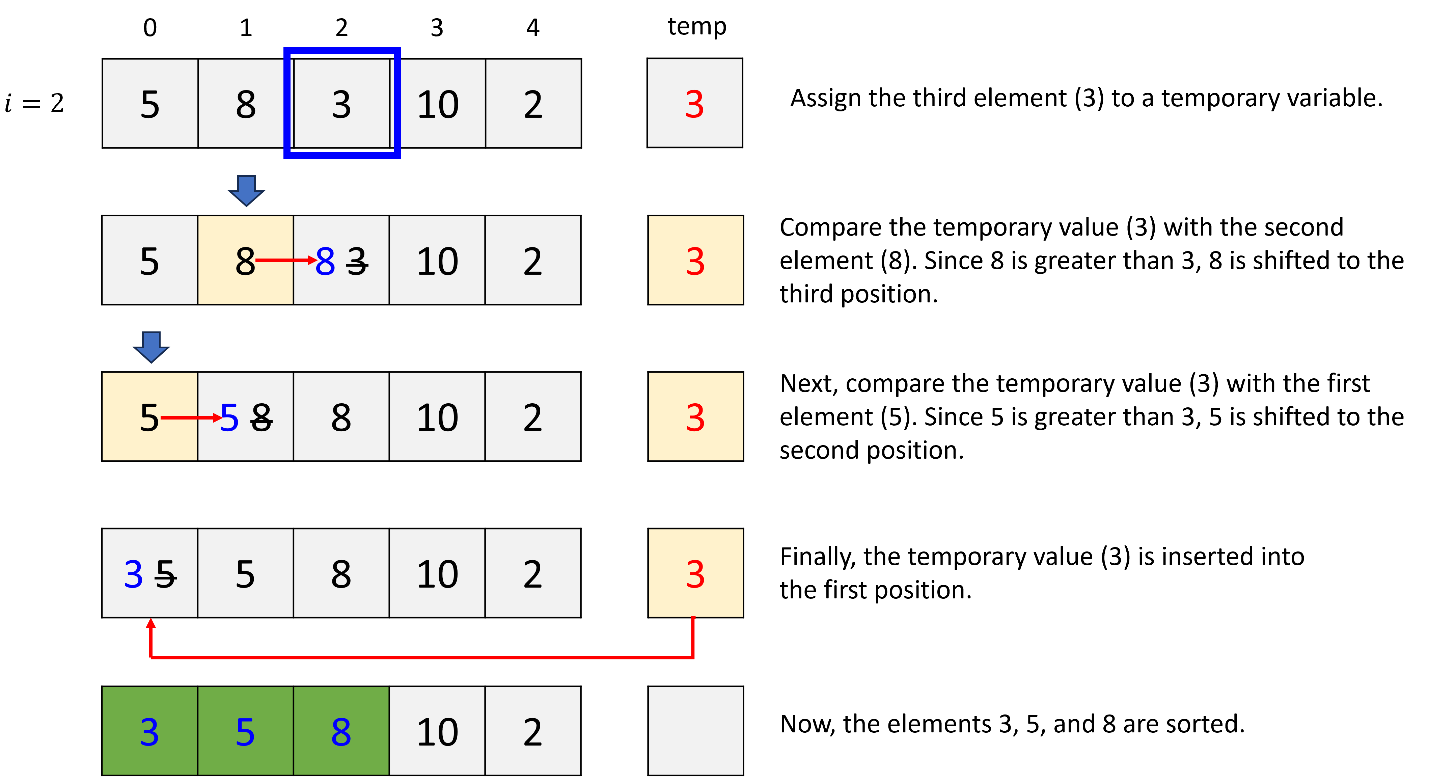
c. 3^rd iteration (i = 3)

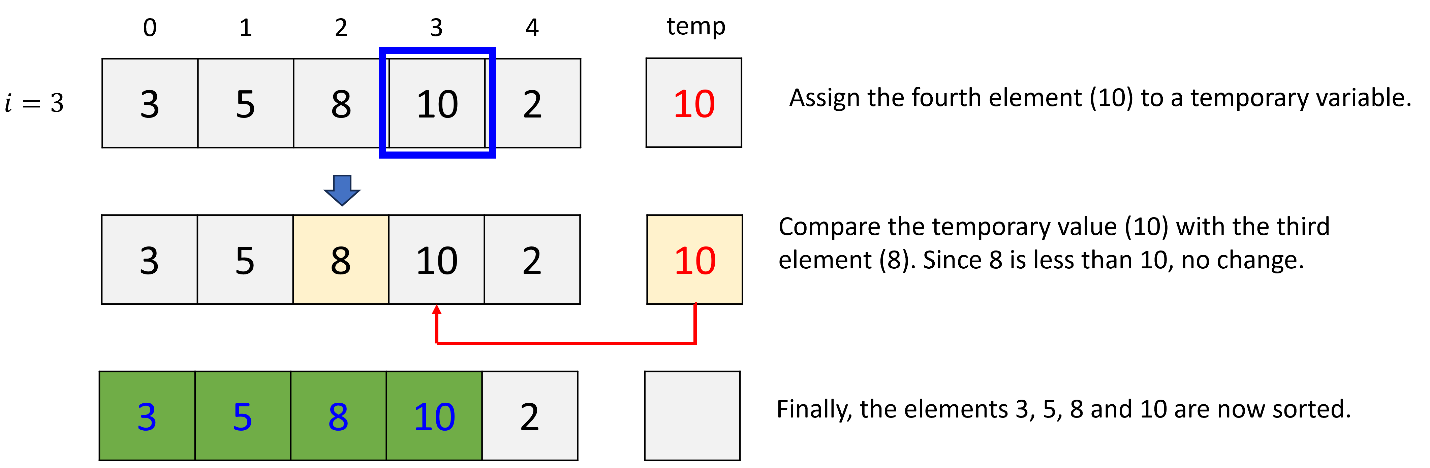
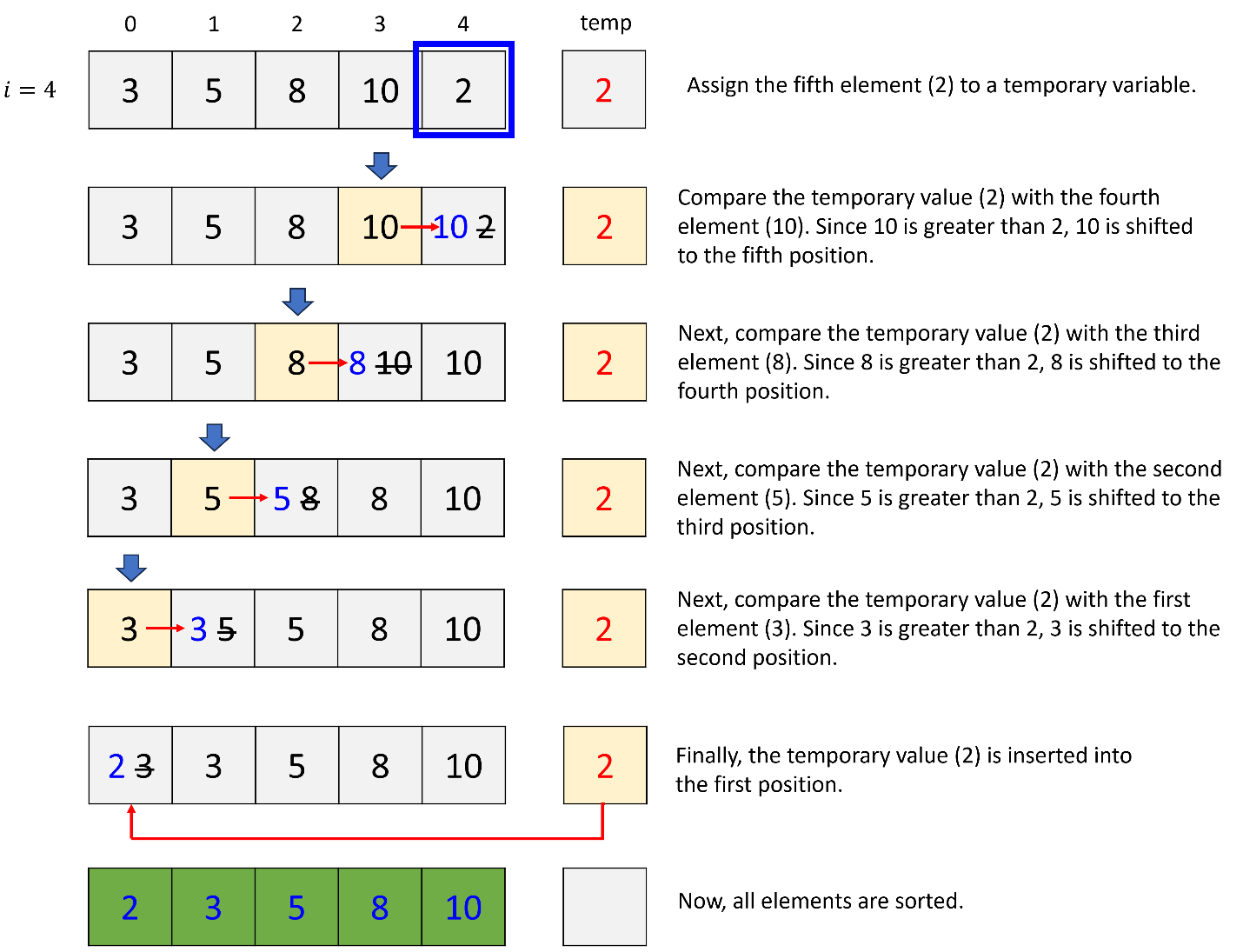
d. 4^th iteration (i = 4)

 

2. Insertion Sort Implementation

Output:

[2, 3, 5, 8, 10]

 

3. Time Complexity 

In the worst-case scenario, where the list is initially in ascending order and requires sorting into descending order, the number of comparisons varies across each iteration. For the first iteration (i = 1), only 1 comparison is necessary, for the second iteration (i = 2), comparisons are needed, and so on until the (n - 1)th iteration. Summing these comparisons yields

Thus, the complexity of the selection sort algorithm in this scenario is O(n²).

Conversely, in the best-case scenario, where the list is already sorted in ascending order and requires sorting into ascending order again, only one comparison is needed per iteration. Hence, there are only n - 1 comparisons in total. Thus, the complexity of the selection sort algorithm in the best-case scenario is O(n).