The selection sort algorithm locates the smallest number within the list and exchanges it with the first element. Subsequently, it identifies the smallest number among the remaining elements and swaps it with the second element, repeating this process until only one number remains.

1. How it works?

Let's say we have a list of elements, and we're attempting to sort the elements in ascending order.

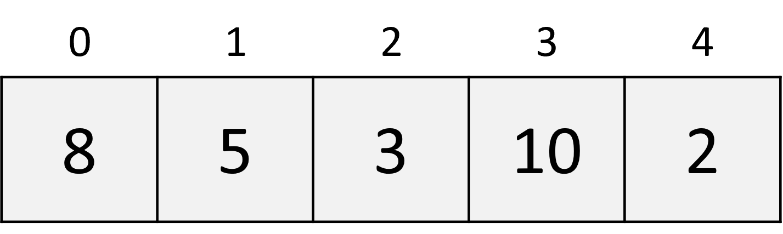
In selection sort, two indices are utilized: one (i) for the iteration and the other (j) for finding the minimum element during each iteration.

 

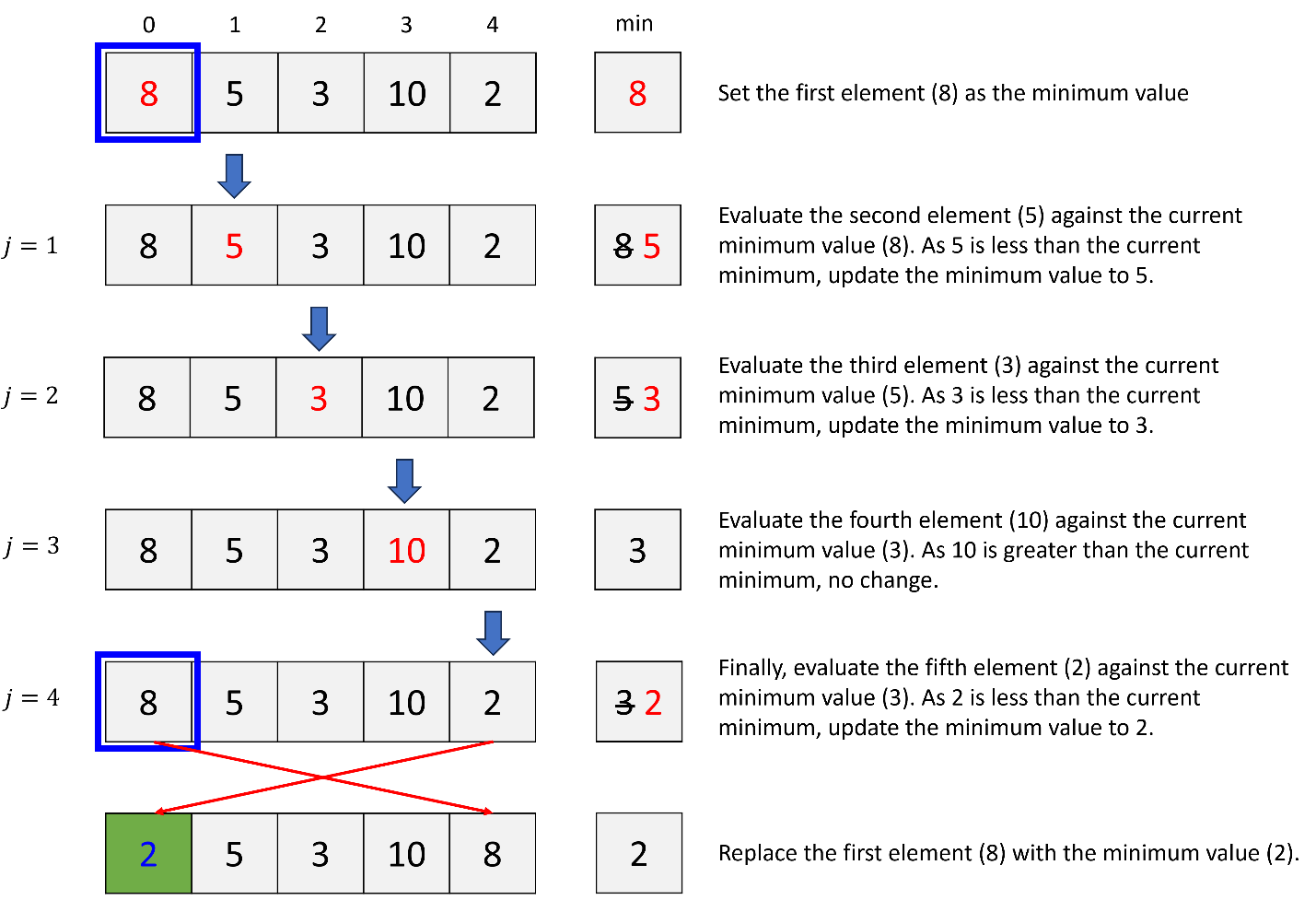
a. 1^st iteration (i = 0)

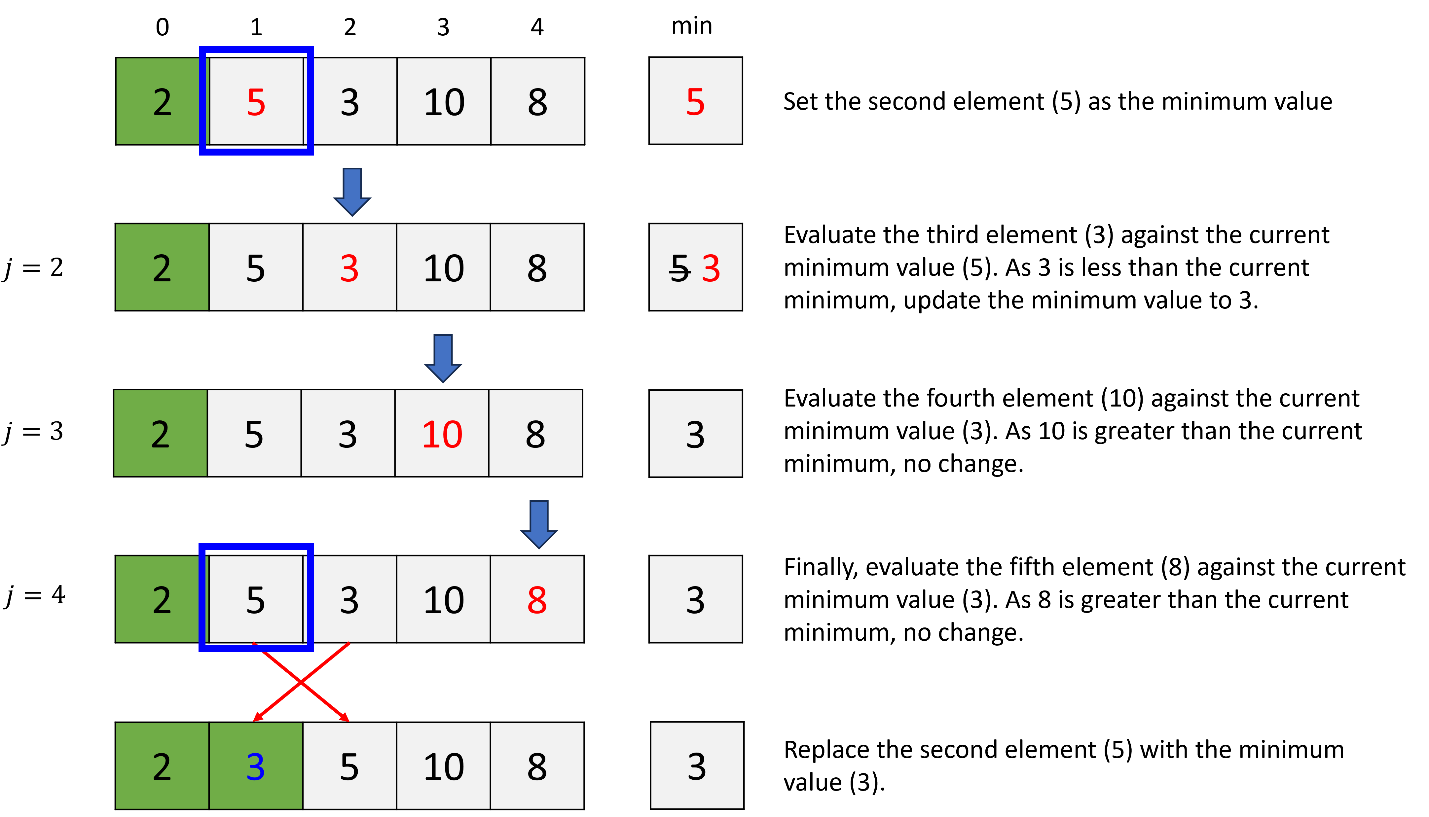
b. 2^nd iteration (i = 1)

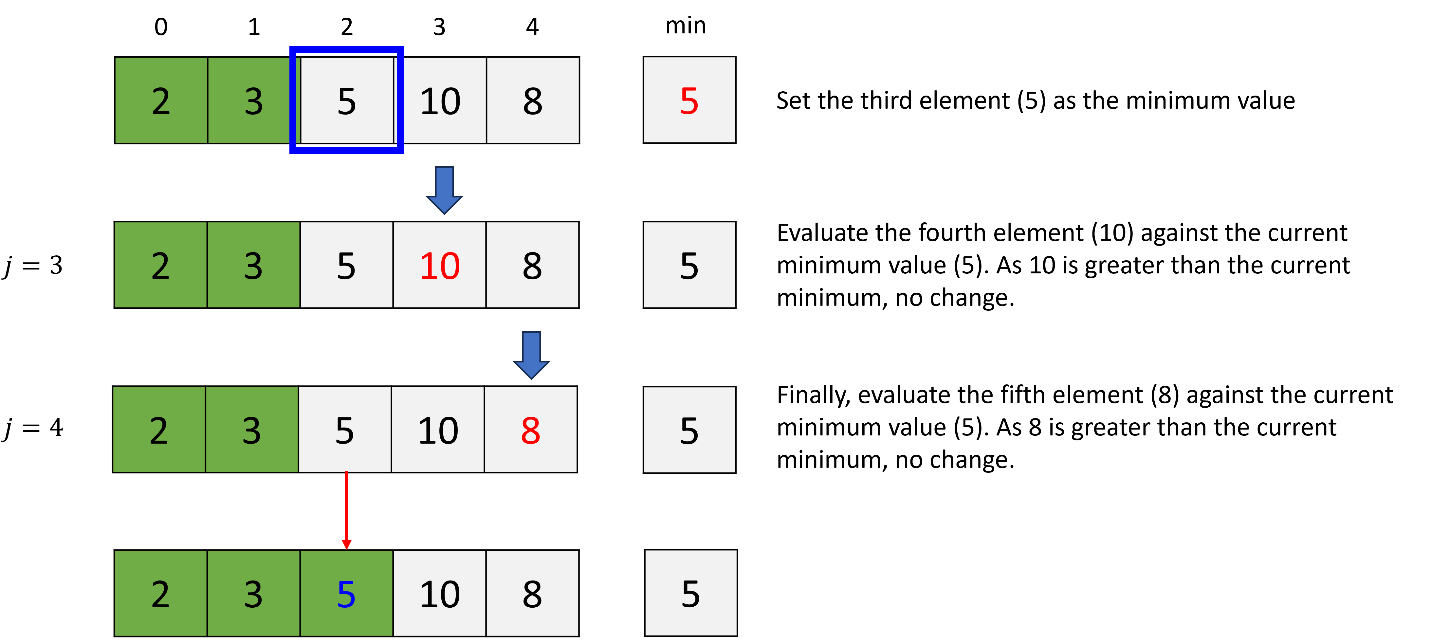
c. 3^rd iteration (i = 2)

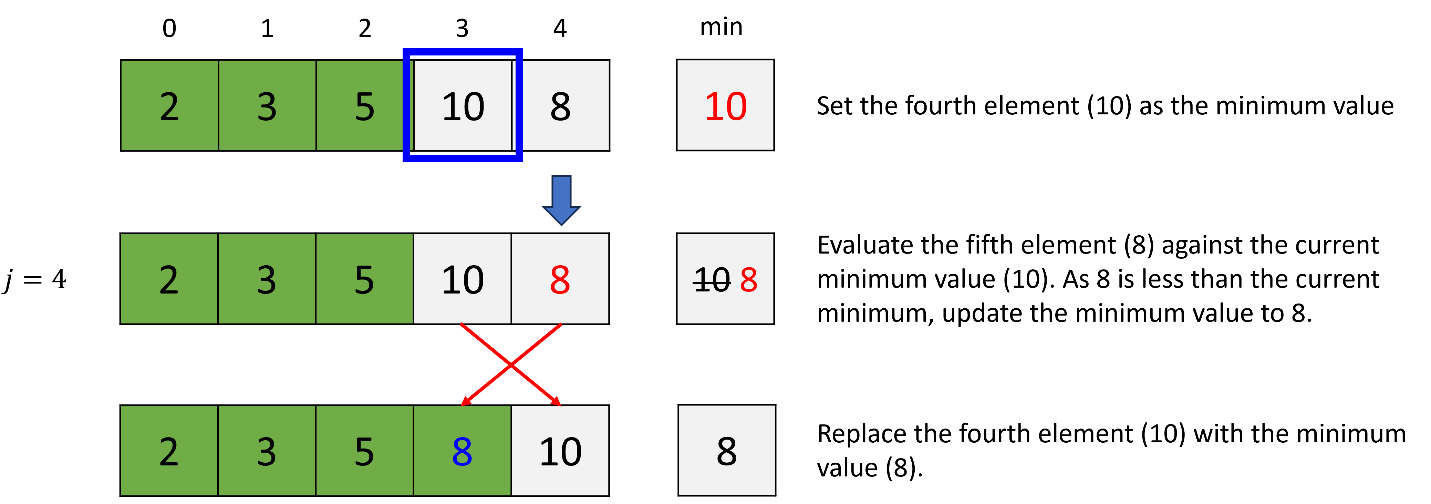
d. 4^th iteration (i = 3)

 

2. Selection Sort Implementation

 

Output:

[2, 3, 5, 8, 10]

 

3. Time Complexity

 

In the selection sort algorithm, during each iteration, the number of comparisons decreases by one. Specifically, in the first pass, there are n - 1 comparisons, in the second pass, n - 2 comparisons, and so on until the last pass with just one comparison. Summing these up, we get

Thus, the complexity of the selection sort algorithm is O(n²).