Binary search is another widely used approach for searching within a list of values. However, for binary search to function correctly, it requires that the elements in the list are already ordered. Assume that the list is in ascending order.

• How it works

To begin, we must designate three indices: 'low', 'mid', and 'high'. 'low' corresponds to the smallest element, 'high' to the largest, and 'mid' is calculated as "(low + high) / 2". We are attempting to find a specific element, which we'll refer to as the "key."

                                                                                                                

  Low                                                          Mid                                                                High

 

Example 1

The following steps are as follows to find key = 31.

Step 1: We begin by comparing the 'mid' element in the list, which is '19', with the key. Since the key, which is 31, is not equal to 19 and greater than 19.

                                                                   31 ≠ 19

                                                                                                                       

Low = 0                                                            Mid = 3                                                        High = 6

 

In Step 2, since the key (31) is greater than 19, we don't need to search the half of the list that is less than the key. Therefore, we update the 'low' and 'mid' indices as follows: 'low = mid + 1 = 3 + 1 = 4', so 'low' indicates 23. 'mid = (low + high) / 2 = (4 + 6) / 2 = 5', which indicates 31. 'high' remains unchanged.

              

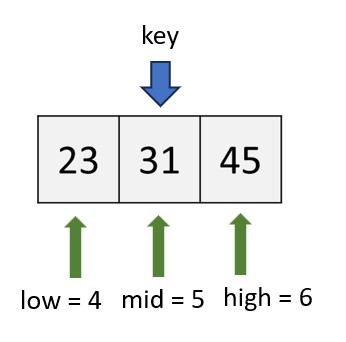
Step 3: Moving forward, we assess the 'mid' element within the list, denoted as '31', in comparison to the key value, which is also 31. Given that the key matches the value of 31, we have successfully identified the desired element.

 

Example 2

The following steps are as follows to find key = 10.

Step 1: We begin by comparing the 'mid' element in the list, which is '19', with the key. Since the key, which is 10, is not equal to 19 and less than 19.

    10 ≠ 19

                                                                                                                      

       Low=0                                                         Mid=3                                                        High=6

 

In Step 2, since the key (10) is less than 19, we don't need to search the half of the list that is greater than the key. Therefore, we update the 'mid' and 'high' indices as follows: 'high = mid - 1 = 3 - 1 = 2', so 'high' indicates 15. 'mid = (low + high) / 2 = (0 + 2) / 2 = 1', which indicates 12. 'low' remains unchanged.

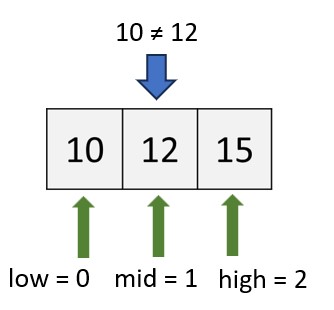
Step 3: Next, we compare the 'mid' element in the list, which is '12', with the key. Since the key, which is 10, is not equal to 12 and less than 12. And update indices as below: 'high = mid - 1 = 1 - 1 = 0', so 'high' indicates 10. 'mid = (low + high) / 2 = (0 + 1) / 2 = 0', which indicates 10. 'low' remains unchanged.

 

Step 4: Moving forward, we assess the 'mid' element within the list, denoted as '10', in comparison to the key value, which is also 10. Given that the key matches the value of 10, we have successfully identified the desired element.

 

• Binary Search Implementation

Example: 1 Search for a number

 

Output:

31 is found at index 5

 

 

Example 2: Search for a string

Output:

Davis is found at index 0

 

• Time Complexity

Let T(n) represent the time complexity for a binary search on a list of n elements. With each comparison, the number of elements is halved.

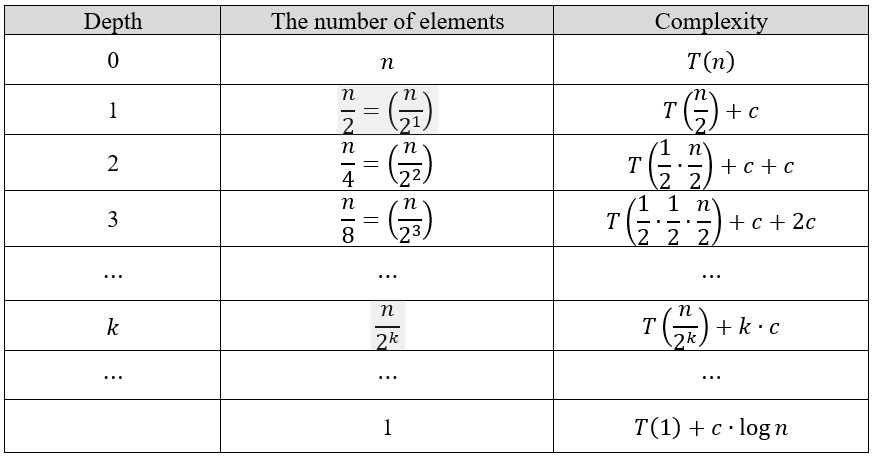
Until the key value is found, indicating that only one element remains, the relationship  holds true, where  represents the initial number of elements and  represents the number of comparisons made. By solving for  in terms of , we find .

Therefore, the number of comparisons made is logarithmic with respect to the initial number of elements, leading to a time complexity of O(log n).