20-4. Quick Sort

Quick sort is a sorting algorithm that utilizes the divide and conquer approach.

The quick sort algorithm operates in the following manner: it chooses a pivot element from the list. Then, it partitions the list into two segments, ensuring that all elements in the first segment are either less than or equal to the pivot, while all elements in the second segment are greater than the pivot. Apply the quick sort algorithm recursively to both the first and second segments.

1. How it works?

Let's say we have a list of elements, and we're attempting to sort the elements in ascending order.

a. Quick sort of all elements:

Firstly, apply the quick sort algorithm to all elements in the list.

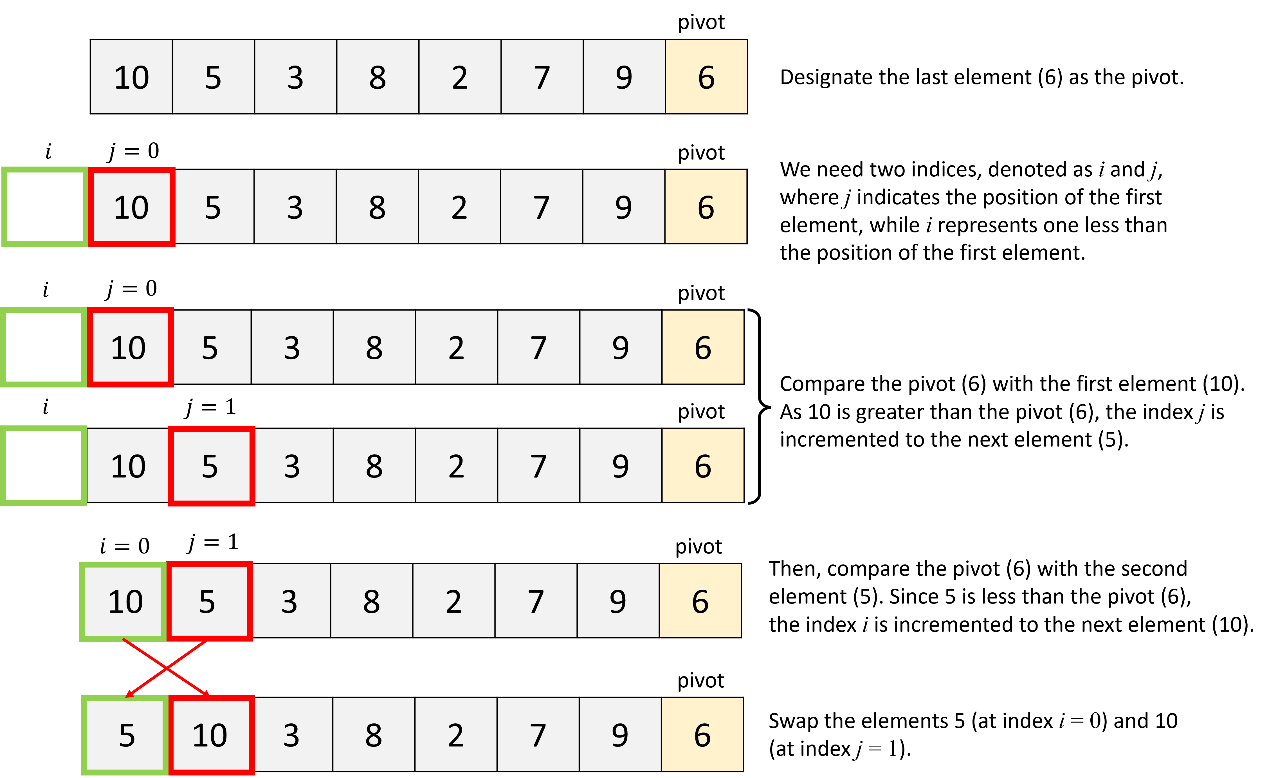
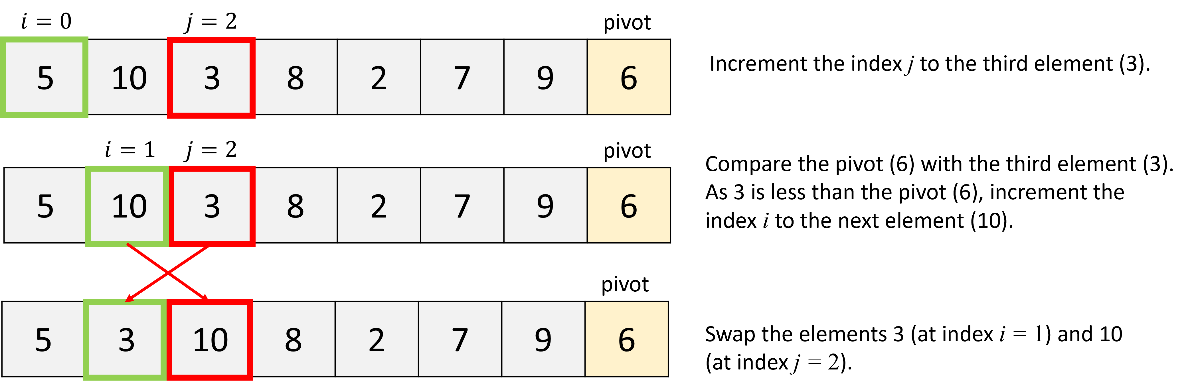
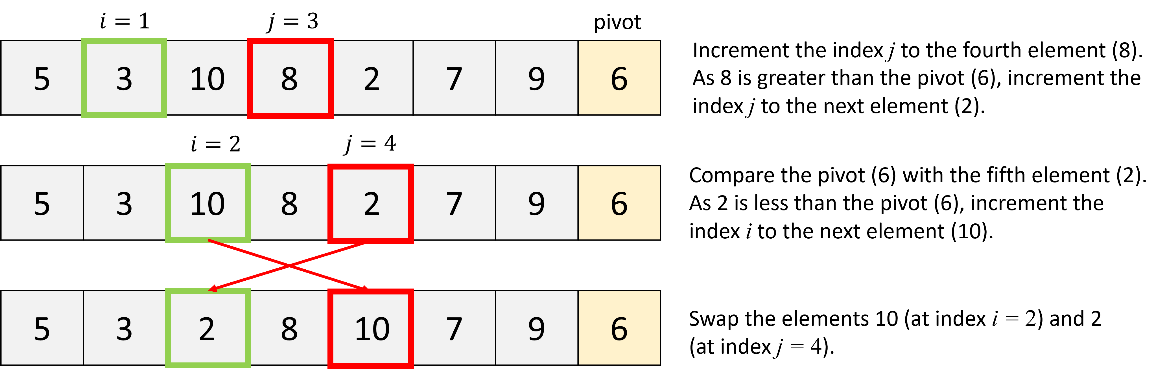
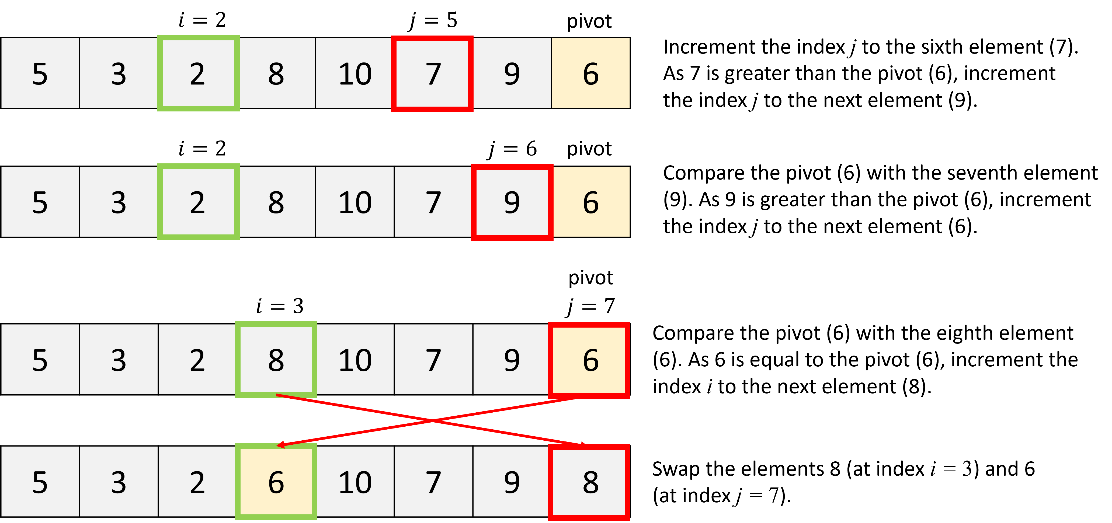
b. Quick sort of the first partition:

Next, apply the quick sort algorithm to the first partition in the list.

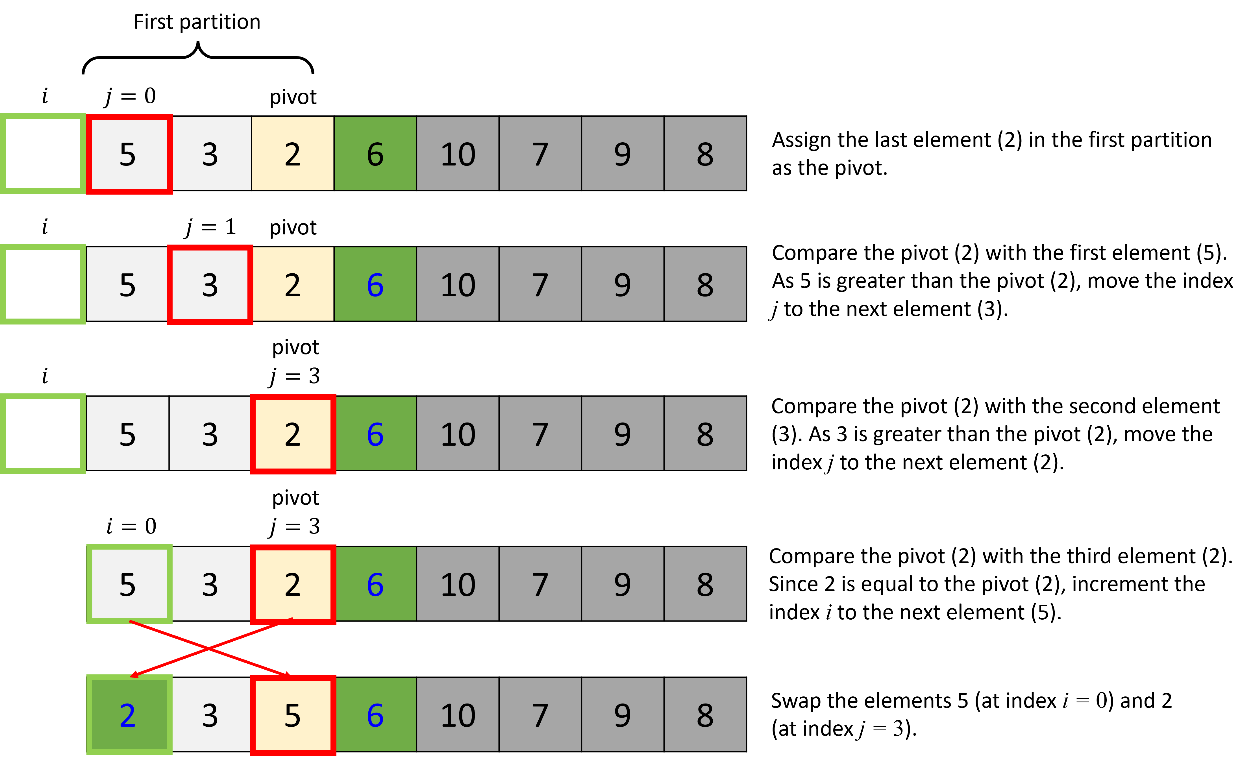
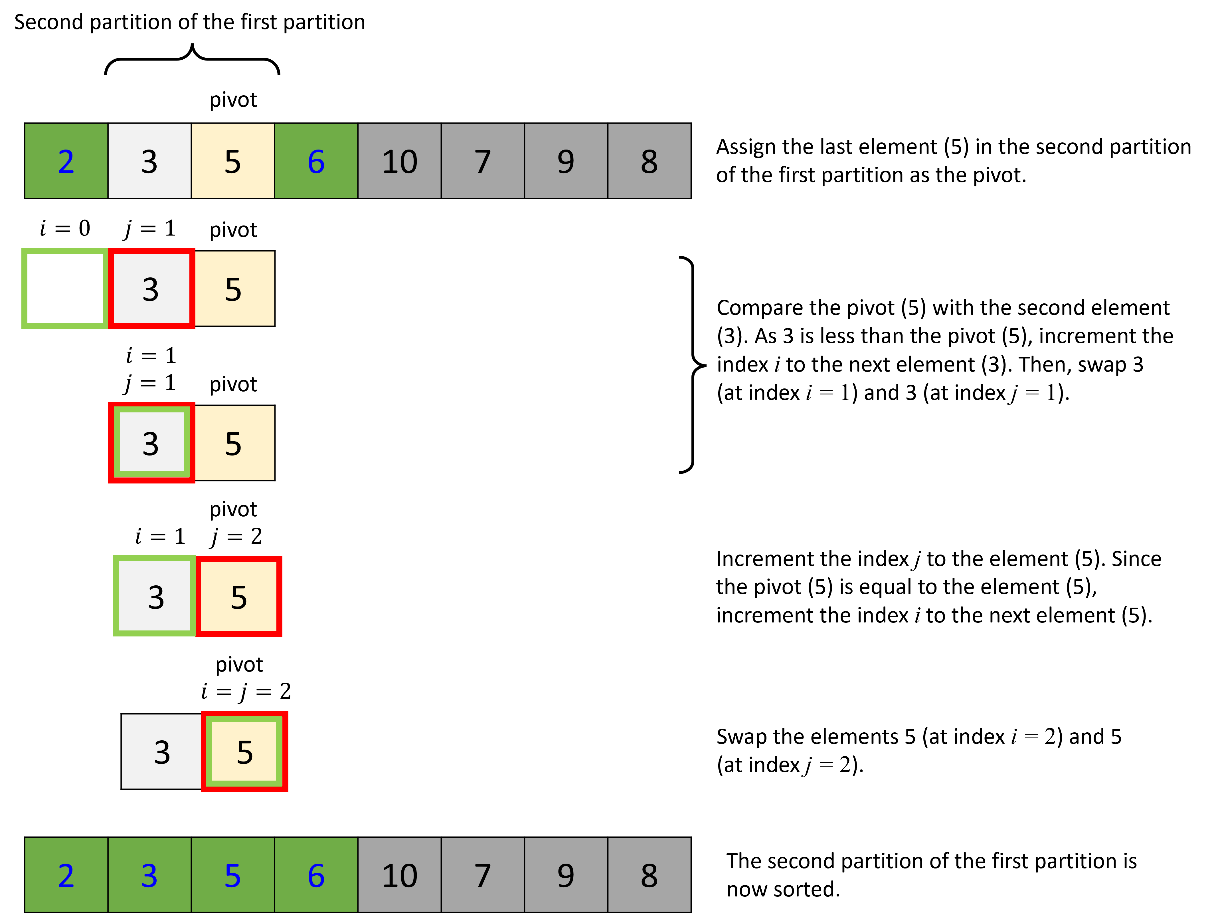
c. Quick sort of the second partition:

Next, apply the quick sort algorithm to the second partition in the list.

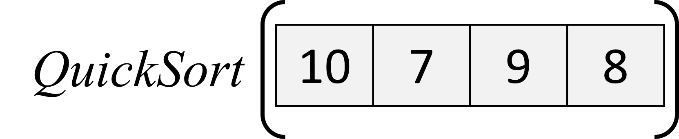
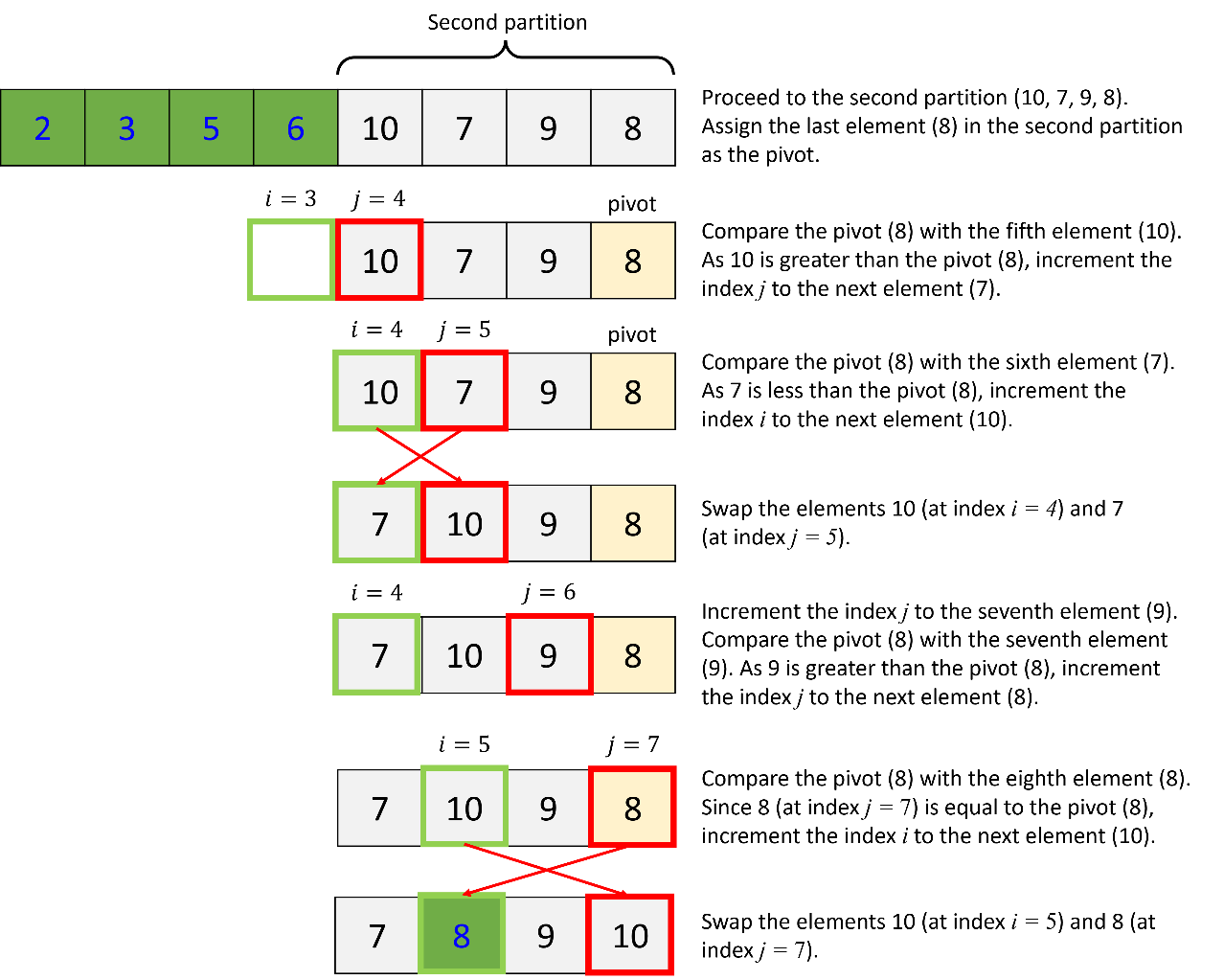
d. Quick sort of the first partition of the second partition:

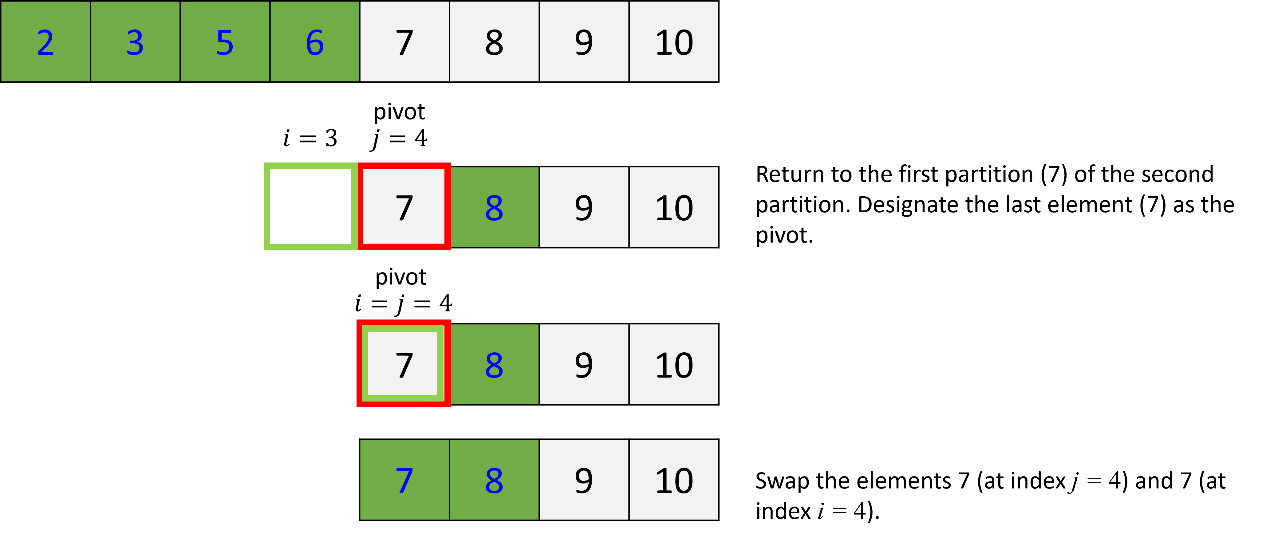
e. Quick sort of the second partition of the second partition:

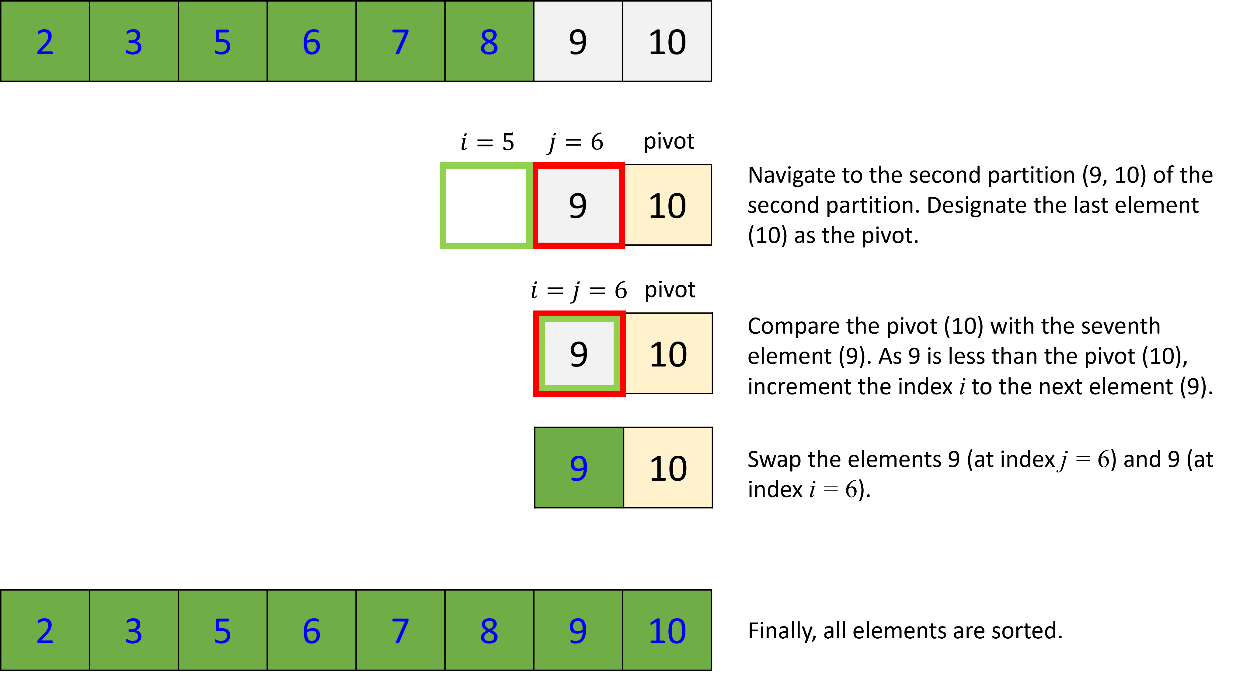
2. Quick Sort Implementation

# function to find the partition position
def partition(array, low, high):

# choose the rightmost element as pivot
    pivot = array[high]

# pointer for greater element
    i = low - 1

# traverse through all elements compare each element with pivot
    for j in range(low, high):
      if array[j] <= pivot:
        # if element smaller than pivot is found
        # swap it with the greater element pointed by i
        i = i + 1

# swapping element at i with element at j
        (array[i], array[j]) = (array[j], array[i])

# swap the pivot element with the greater element specified by i
    (array[i + 1], array[high]) = (array[high], array[i + 1])

# return the position from where partition is done
    return i + 1

# function to perform quicksort
def quickSort(array, low, high):
    if low < high:

# find pivot element such that
      # element smaller than pivot are on the left
      # element greater than pivot are on the right
      pi = partition(array, low, high)

# recursive call on the left of pivot
      quickSort(array, low, pi - 1)

# recursive call on the right of pivot
      quickSort(array, pi + 1, high)

def main():
    
    data = [10, 5, 3, 8, 2, 7, 9, 6]

size = len(data)

quickSort(data, 0, size - 1)

print('Sorted Array in Ascending Order:')
    print(data)

main()

Output:

[2, 3, 5, 6, 7, 8, 9, 10]

3. Time Complexity

In the worst-case scenario, each time the pivot is chosen, it divides the list into one large sublist and another empty sublist. The size of the larger sublist is one less than the size of the previous sublist. Thus, the complexity of the quick sort algorithm in this scenario is O(n²).

In the best case, each time the pivot is selected, it divides the array into two approximately equal-sized parts. Let T(n) denote the time required for sorting an array of elements using quicksort.

Hence,

The complexity is O(n log n).

Last updated: April 23, 2025

Python Programming

20-4. Quick Sort