A stack represents a linear data structure adhering to the Last In First Out (LIFO) principle. Elements are accessed, inserted, and deleted from the end, commonly referred to as the top, of the stack.

How it works?

1) Add elements to a stack

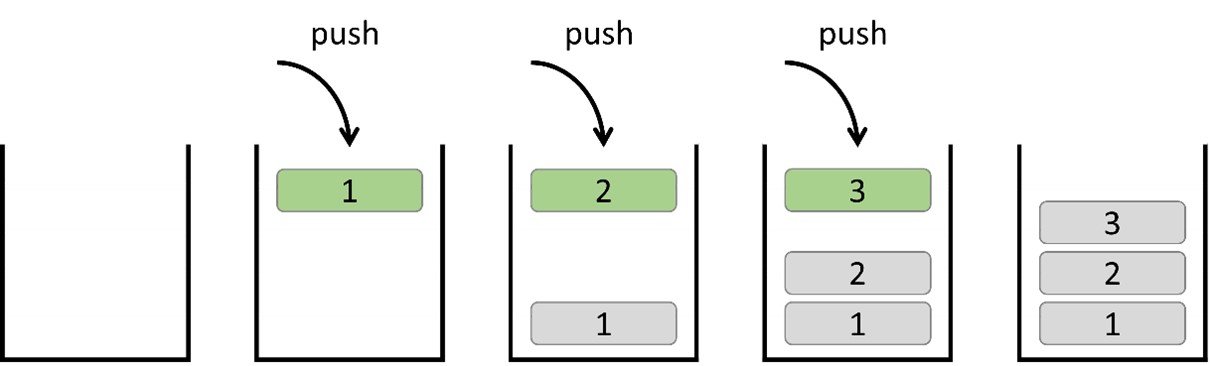
When an element (1) is added, it is stacked at the bottom. Subsequently, when a new element (2) is added, it is stacked on top of element (1). Following this, when a new element (3) is added, it is stacked on top of element (2).

2) Remove elements from a stack

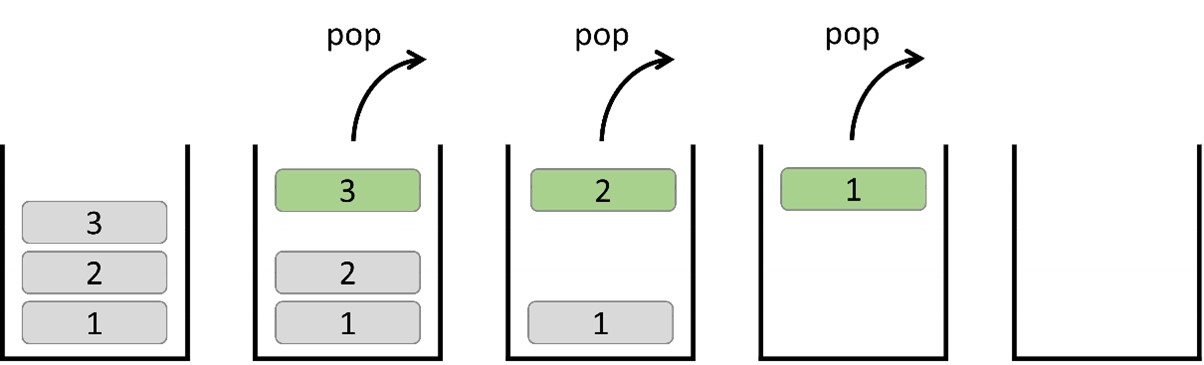
When an element is removed, the top element (3) is extracted from the stack. Subsequently, the top element (2) is removed, followed by the removal of the top element (1).

Basic operations of a stack

• Push: Add an element to the top of a stack
• Pop: Remove an element from the top of a stack
• isEmpty: Check if the stack is empty
• peek: Get the value of the top element without removing it
• getSize: Return the size of the stack

Stack Implementation

The stack is implemented using a list, where the top of the stack corresponds to the right end (last item) of the list.

Test Program

Output:

9 8 7 6 5 4 3 2 1 0

 

If we designate the top of the stack as the first item of the list, we can use insert(0, item) to add items and pop(0) to remove items.

 

Performance difference depending on the implementation method:

 

Output:

9 8 7 6 5 4 3 2 1 0

 

Time to add elements to Stack:

10000 takes: 0.0019941329956054688 20000 takes: 0.002992391586303711 30000 takes: 0.007980585098266602 40000 takes: 0.0199429988861084 50000 takes: 0.03391575813293457 70000 takes: 0.018947362899780273 80000 takes: 0.055847883224487305 90000 takes: 0.04089236259460449 100000 takes: 0.03391218185424805

 

Time to remove elements from Stack:

10000 takes: 0.009983301162719727 20000 takes: 0.030913829803466797 30000 takes: 0.0279233455657959 40000 takes: 0.05086517333984375 50000 takes: 0.03774094581604004 60000 takes: 0.06283450126647949 70000 takes: 0.058838844299316406 80000 takes: 0.06280803680419922 90000 takes: 0.06582164764404297 100000 takes: 0.059885501861572266

 

Time to add elements to StackLeft:

10000 takes: 0.08074545860290527 20000 takes: 0.23097586631774902 30000 takes: 0.4888572692871094 40000 takes: 0.9527907371520996 50000 takes: 1.3121168613433838 60000 takes: 1.972851276397705 70000 takes: 2.676400899887085 80000 takes: 3.048536777496338 90000 takes: 5.077842473983765 100000 takes: 5.5361456871032715

 

Time to remove elements from StackLeft:

10000 takes: 0.02091217041015625 20000 takes: 0.05186033248901367 30000 takes: 0.1226654052734375 40000 takes: 0.2274796962738037 50000 takes: 0.3652002811431885 60000 takes: 0.8326921463012695 70000 takes: 0.8500213623046875 80000 takes: 1.1882421970367432 90000 takes: 1.5454580783843994 100000 takes: 2.1574411392211914

 

• Stack Applications

Paring parenthesis in a string:

The parentheses used for function or operation execution must be properly paired. That is, each opening parenthesis must have a corresponding closing parenthesis.

If we only consider parentheses in the expression, we can easily confirm that all parentheses are properly paired in the following pattern:

()()()()

However, it becomes more complicated when parentheses are nested:

(()()()()()) ((((())))) (()((())()))

For example, the following example contains unmatched parentheses:

(((((((()) (())) (()()(()

The following code implements a function using a stack to determine whether a string consisting of parentheses is composed of properly paired parentheses. The usage of the stack is as follows: Starting from the left of the string, when encountering an opening parenthesis or a closing parenthesis, repeat the following actions:

• Opening parenthesis: Add to the stack.
• Closing parenthesis: Remove the top item from the stack.

Through these actions, three cases may occur:

• The stack becomes empty before the entire string is checked: There are too many closing parentheses.
• The stack is not empty after checking the entire string: There are too many opening parentheses.
• Otherwise, all parentheses are properly paired.

Output:

True True False False

 

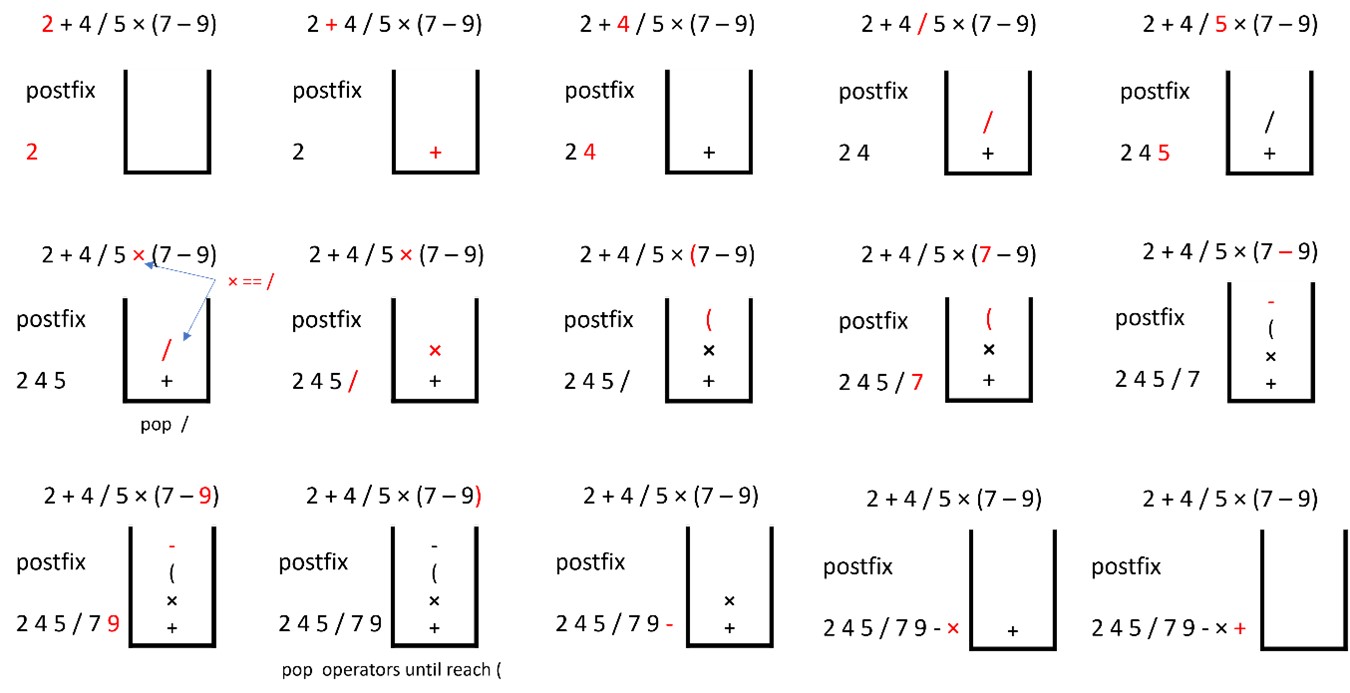
Convert infix to postfix using a stack:

In the process of converting an infix expression to a postfix expression, the operands maintain their order, while the arrangement of operators is determined by the precedence of operators and the execution order defined by parentheses. This property is leveraged in the development of an algorithm for converting notation.

Proceeding sequentially from the left of the infix expression, we examine each operand and operator encountered. Operand elements are directly appended to the postfix expression. Operators, on the other hand, are managed using a separate stack. However, considering operator precedence and the presence of parentheses, the stack may be manipulated prior to adding the operator to it.

The reason for utilizing a stack to manage operators is to ensure proper execution order.

• When a lower-priority operator is encountered compared to the one already present in the stack, it indicates that calculations related to the higher or equal priority operator in the stack should be performed first.
• This necessitates the removal of those higher-priority operators from the stack and their immediate addition to the postfix expression.
• Moreover, in scenarios involving parentheses, such as in expressions like (A + B) * C, opening parentheses are also pushed onto the stack.
• Conversely, upon encountering a closing parenthesis, the process entails popping operators from the stack until an opening parenthesis is encountered, thereby progressively constructing the postfix expression.

 

Convert infix to postfix:

 

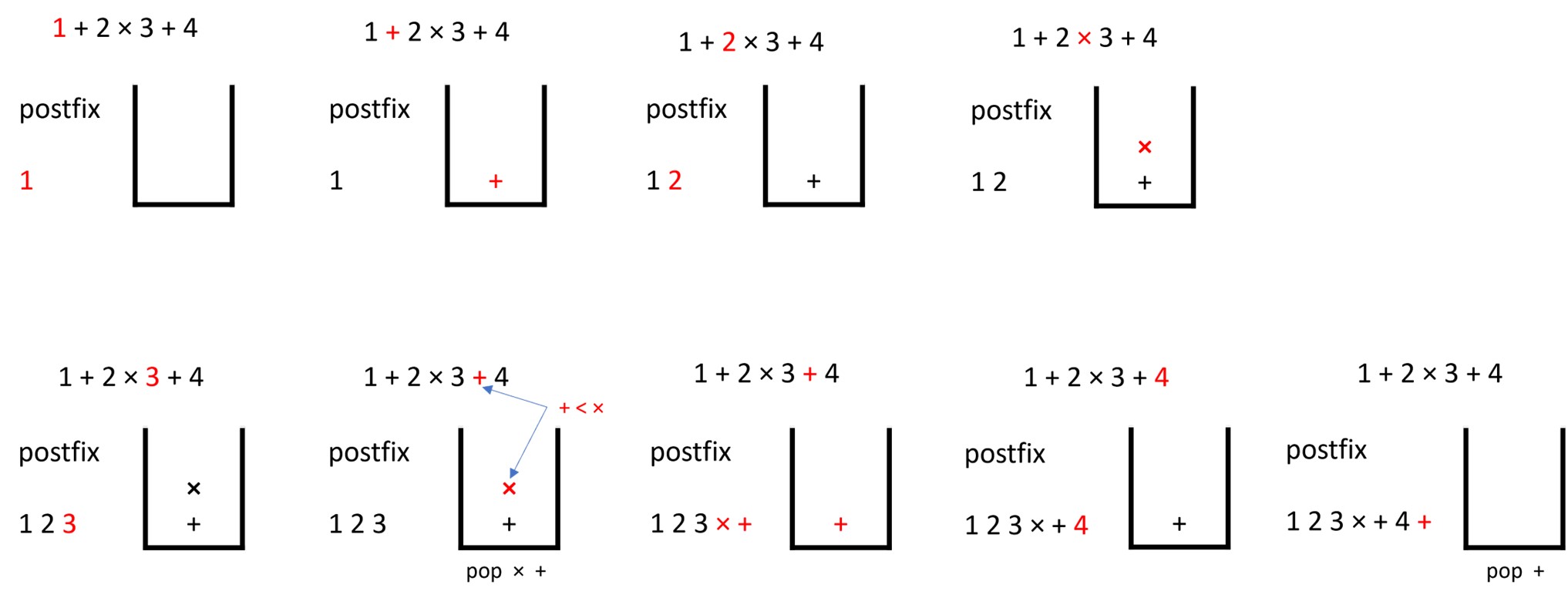
Example 1: 1 + 2 × 3 + 4

 

 

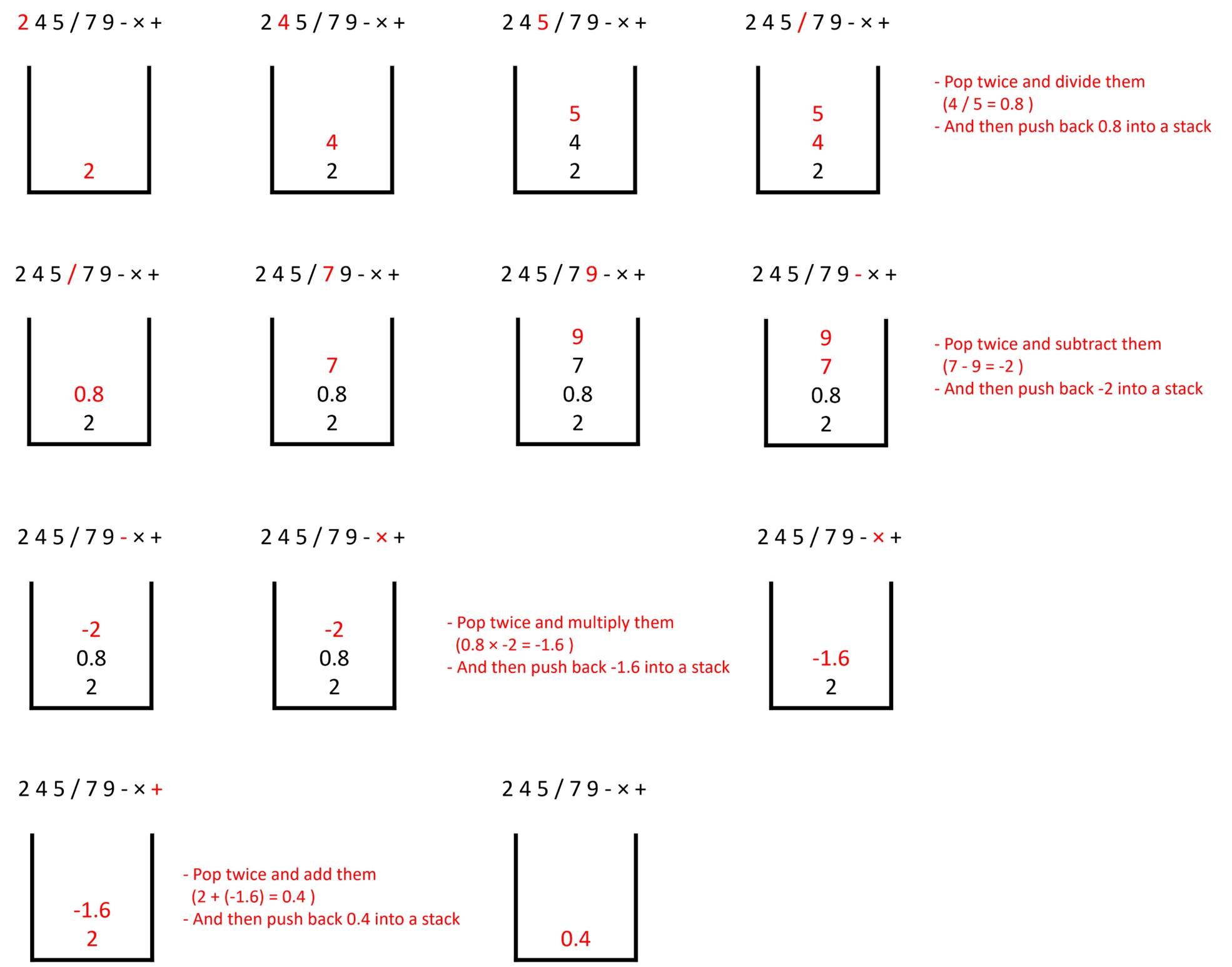
Example: 2 + 4 / 5 × (7 – 9)

 

 

Calculate using postfix

 

Example: 1 2 3 × + 4 +

 

 

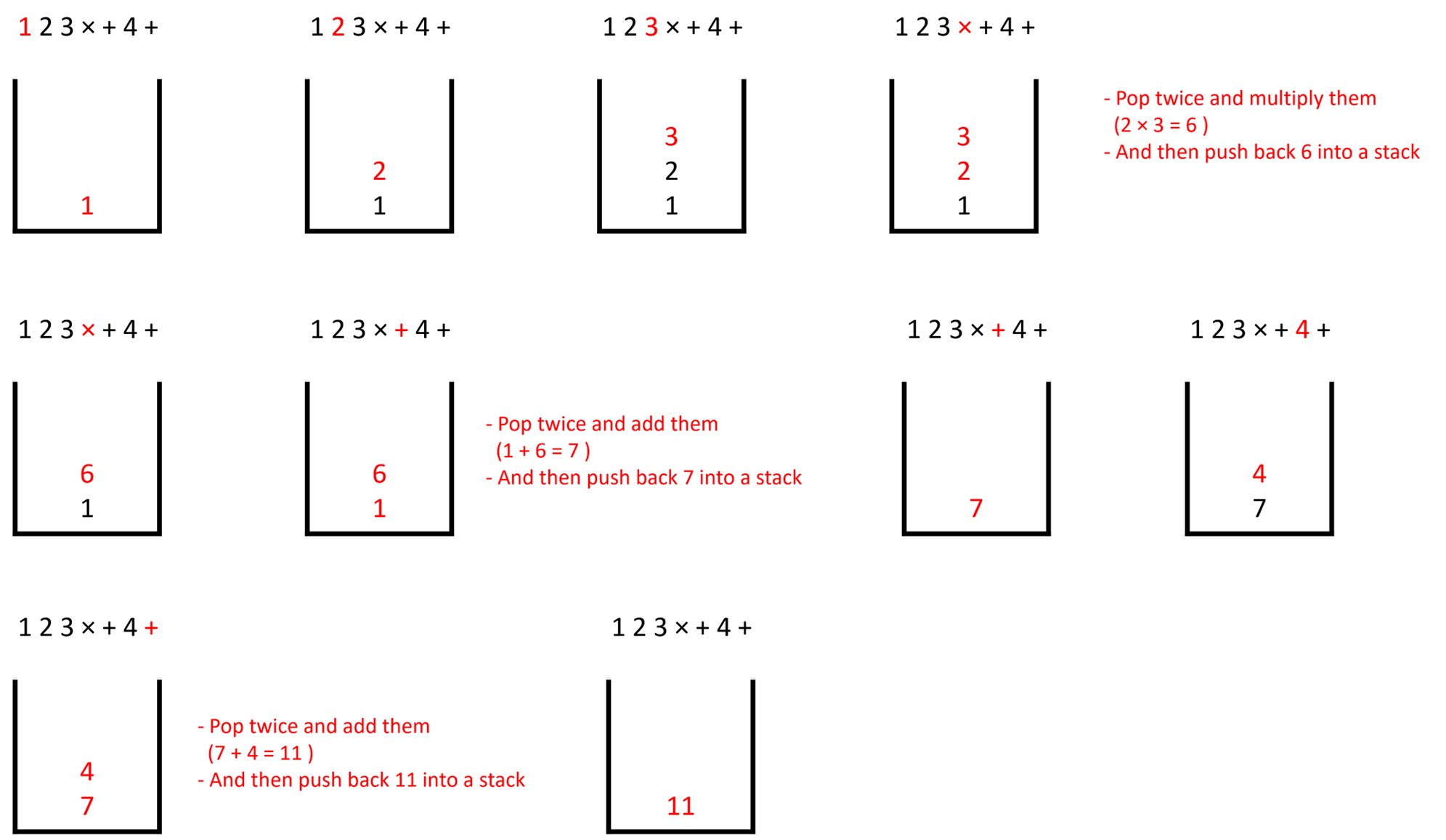
Example: 2 4 5 / 7 9 - × +