20-5. Merge Sort

The Merge sort algorithm operates recursively in the following manner: it divides the list into two halves and recursively applies merge sort to each half. Once both halves are sorted, the algorithm merges them together.

1. How it works?

Let's say we have a list of elements, and we're attempting to sort the elements in ascending order.

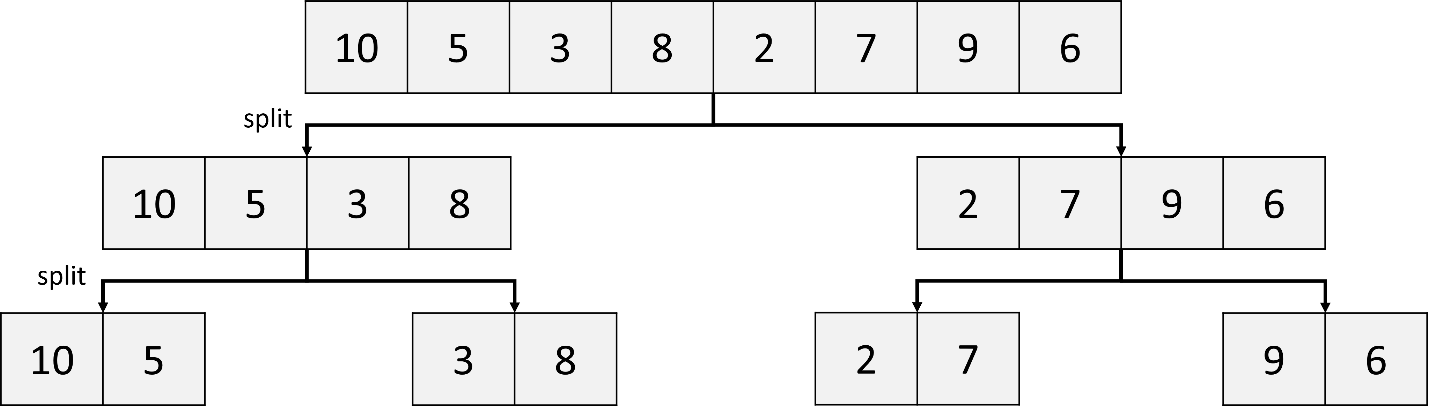
a. Divide a list into two sublists (left half and right half):

Initially, a list of elements (10, 5, 3, 8, 2, 7, 6) is divided into two sublists. The left sublist consists of (10, 5, 3, 8), while the right sublist comprises (2, 7, 9, 6).

b. Divide each sublist into two sublists, recursively:

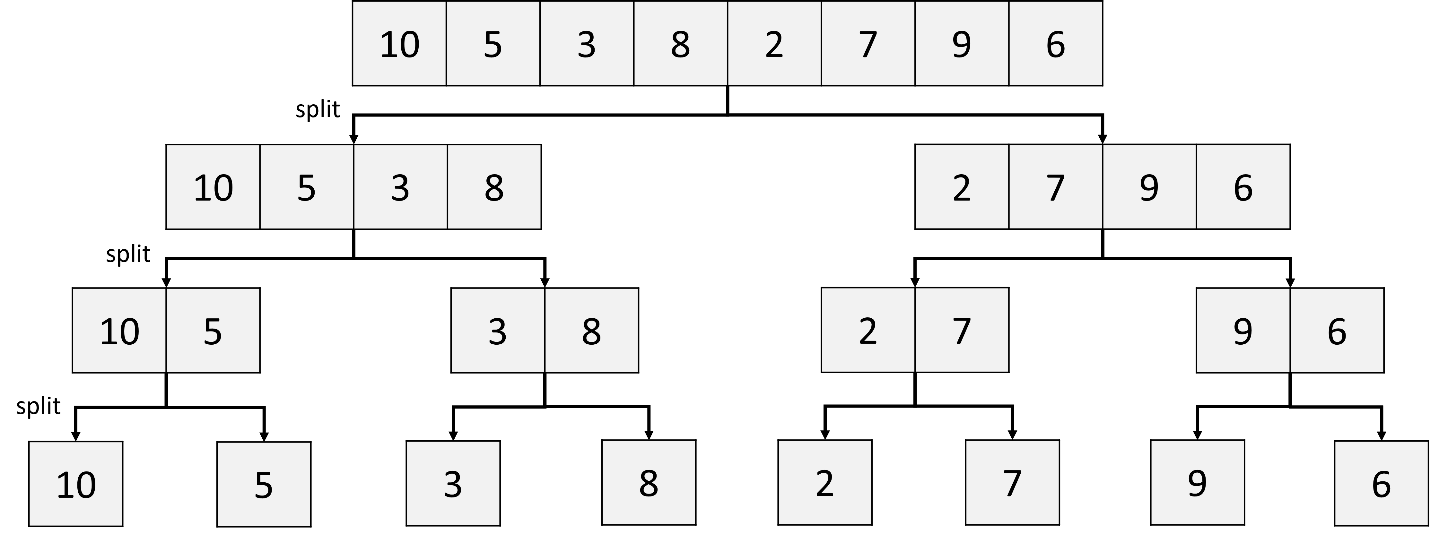
c. Merge two sublists: (10), (5); (3), (8); (2), (7); (9), (6)

Compare 10 and 5. Since 5 is less than 10, 5 is placed first in a new sorted list, followed by 10.
Compare 3 and 8. Since 3 is less than 8, 3 is placed first in a new sorted list, followed by 8.
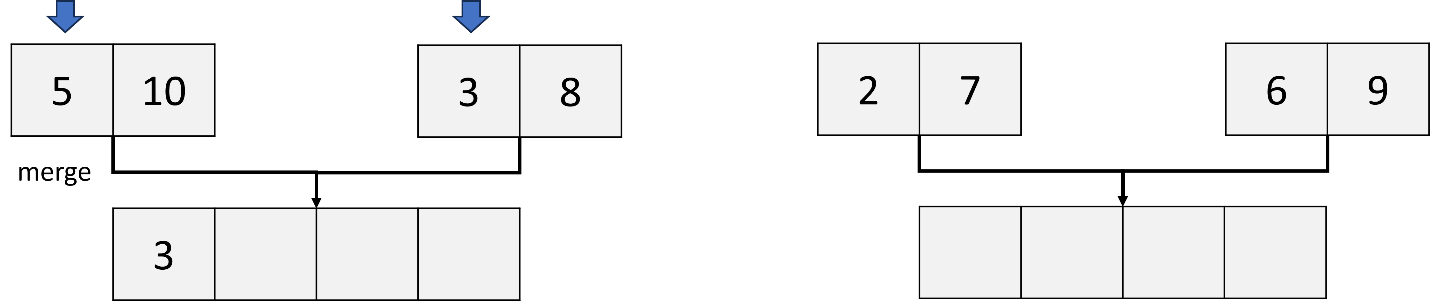
Merge the sublists: (2, 7) and (6, 9).

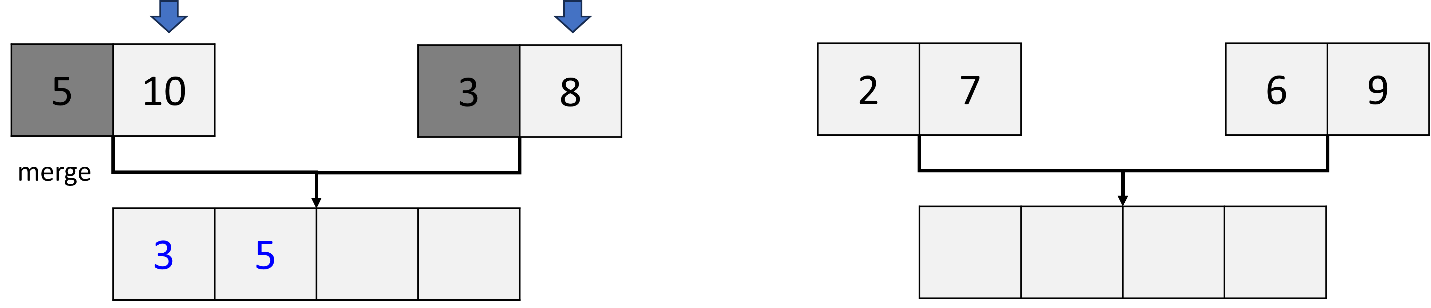
d. Merge two sublists, (5,10), (3,8); (2,7), (6,9):

Compare the first element (5) in the left sublist and the first element (3) in the right sublist. Since 3 is less than 5, 3 is placed first in a new sorted list.

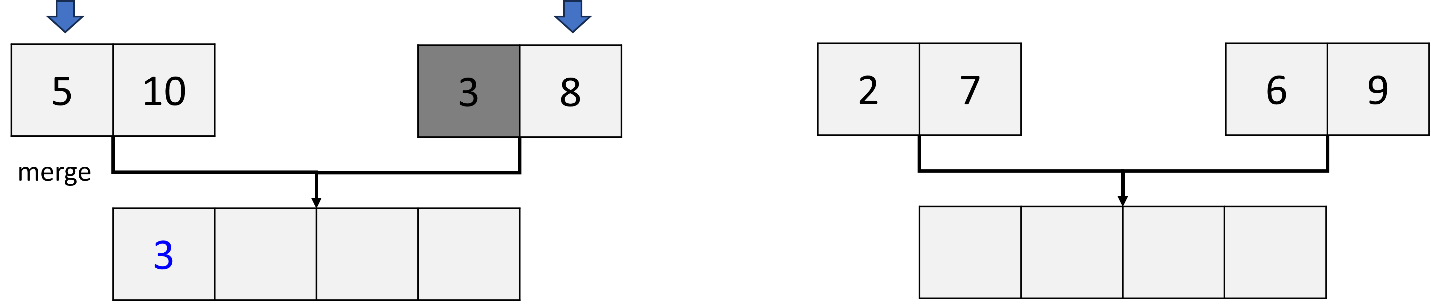
Move to the next element (8) in the right sublist. Compare the first element (5) in the left sublist with the second element (8) in the right sublist. Since 5 is less than 8, 5 is placed second in a new sorted list.

Move to the next element (10) in the left sublist. Compare the second element (10) in the left sublist with the second element (8) in the right sublist. Since 8 is less than 10, 8 is placed third in a new sorted list.

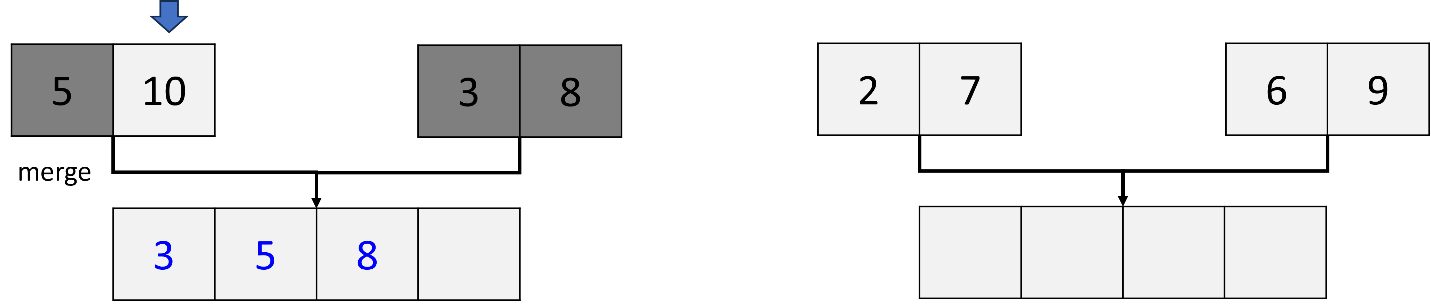
Finally, place the remaining element (10) from the left sublist into the last position in the new sorted list.

Similarly, the right sublists (2, 7) and (6, 9) are sorted as follows:

e. Merge two sublists, (3, 5,8, 10); (2, 6, 7, 9):

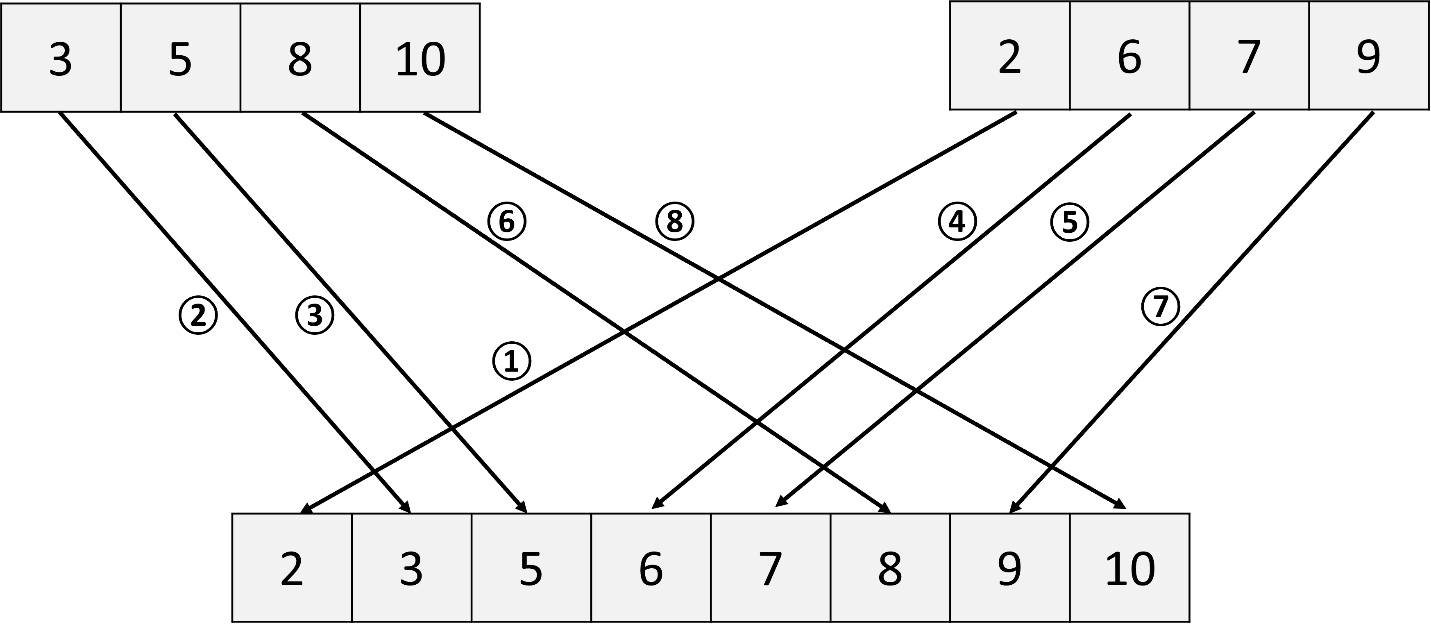
Similarly, compare elements in the sublist (3, 5, 8, 10) with the sublist (2, 6, 7, 9), and then place the smallest element into a new sorted list.

2. Merge Sort Implementation

def mergeSort(array):
    if len(array) > 1:

#  r is the point where the array is divided into two subarrays
        r = len(array)//2
        L = array[:r]
        M = array[r:]

# Sort the two halves
        mergeSort(L)
        mergeSort(M)

i = j = k = 0

# Until we reach either end of either L or M, pick larger among
        # elements L and M and place them in the correct position at  
          A[p..r]
        while i < len(L) and j < len(M):
            if L[i] < M[j]:
                array[k] = L[i]
                i += 1
            else:
                array[k] = M[j]
                j += 1
            k += 1

# When we run out of elements in either L or M,
        # pick up the remaining elements and put in A[p..r]
        while i < len(L):
            array[k] = L[i]
            i += 1
            k += 1

while j < len(M):
            array[k] = M[j]
            j += 1
            k += 1

# Print the array
def printList(array):
    for i in range(len(array)):
        print(array[i], end=" ")
    print()
    
def main():

data = [10, 5, 3, 8, 2, 7, 9, 6]

mergeSort(data)

print("Sorted array is: ")
    printList(data)

main()

Output:

2 3 5 6 7 8 9 10

3. Time Complexity

Let T(n) denote the time required for sorting an list of elements using merge sort. The merge sort algorithm divides the list into two sublists, sorts the sublists using the same algorithm recursively, and then merges the sublists. Therefore,

where 2n-1 represents the time for merging. Thus, the complexity is O(n log n).

Last updated: April 23, 2025

Python Programming

20-5. Merge Sort