Module 17. Stacks and Queues

Learning Objectives

Understand the concept of a stack data structure and its fundamental properties.
Learn how to implement a stack in Python using built-in data structures like lists or arrays.
Explore the basic operations of a stack: push (adding an item), pop (removing the top item), peek (viewing the top item without removal), and isEmpty (checking if the stack is empty).
Understand the concept of a queue data structure and its fundamental properties.
Learn how to implement a queue in Python using built-in data.
Explore the basic operations of a queue: enqueue (adding an item), dequeue (removing the front item), peek (viewing the front item without removal), and isEmpty (checking if the queue is empty).
Understand the concept of a priority queue data structure and its fundamental properties.
Learn how to implement a priority queue in Python using built-in data structures like list, heapq module, and priority queue implementations.
Understand the concept of a deque (double-ended queue) data structure and its fundamental properties.
Learn how to implement a deque in Python using the built-in collections.deque class.
Explore the basic operations of a deque: adding and removing elements from both ends (front and rear), peeking at elements without removal, and checking if the deque is empty.

1. Stacks

A stack represents a linear data structure adhering to the Last In First Out (LIFO) principle. Elements are accessed, inserted, and deleted from the end, commonly referred to as the top, of the stack.

How it works?

1) Add elements to a stack

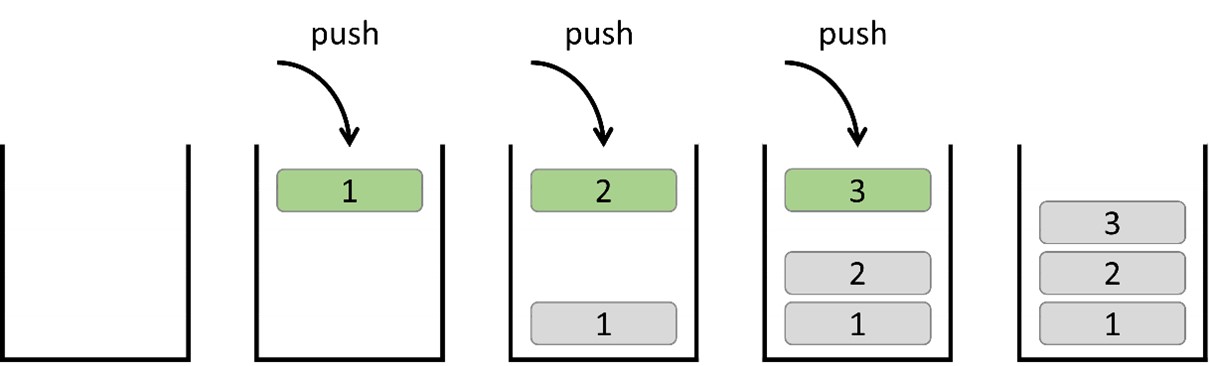
When an element (1) is added, it is stacked at the bottom. Subsequently, when a new element (2) is added, it is stacked on top of element (1). Following this, when a new element (3) is added, it is stacked on top of element (2).

2) Remove elements from a stack

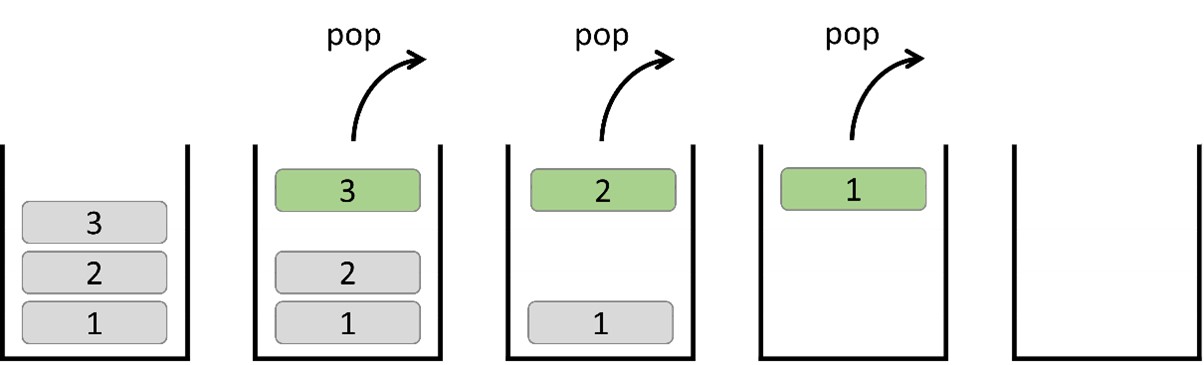
When an element is removed, the top element (3) is extracted from the stack. Subsequently, the top element (2) is removed, followed by the removal of the top element (1).

Basic operations of a stack

Push: Add an element to the top of a stack
Pop: Remove an element from the top of a stack
isEmpty: Check if the stack is empty
peek: Get the value of the top element without removing it
getSize: Return the size of the stack

Stack Implementation

The stack is implemented using a list, where the top of the stack corresponds to the right end (last item) of the list.

Test Program

Output:

9 8 7 6 5 4 3 2 1 0

If we designate the top of the stack as the first item of the list, we can use insert(0, item) to add items and pop(0) to remove items.

Performance difference depending on the implementation method:

import time
from Stack import Stack
from StackLeft import StackLeft

### Push to Stack
print("1) Time to add elements to Stack")
for num in range(10000, 100001, 10000):
    s1 = Stack()
    
    start = time.time()

for item in range(num):
        s1.push(item)

end = time.time()

print(f"{num} takes: {end - start}")

print()
### Push to Stack
print("2) Time to remove elements from Stack")
for num in range(10000, 100001, 10000):
    s2 = Stack()
    
    for item in range(num):
        s2.push(item)

start = time.time()

while not s2.isEmpty():
        s2.pop()

end = time.time()

print(f"{num} takes: {end - start}")

print()
### Push to StackLeft
print("3) Time to add elements to StackLeft")
for num in range(10000, 100001, 10000):
    s3 = StackLeft()
    
    start = time.time()

for item in range(num):
        s3.push(item)

end = time.time()

print(f"{num} takes: {end - start}")

print()
### Push to Stack
print("4) Time to remove elements from StackLeft")
for num in range(10000, 100001, 10000):
    s4 = StackLeft()
    
    for item in range(num):
        s4.push(item)

start = time.time()

while not s4.isEmpty():
        s4.pop()

end = time.time()

print(f"{num} takes: {end - start}")

Output:

9 8 7 6 5 4 3 2 1 0

Time to add elements to Stack:

10000 takes: 0.0019941329956054688

20000 takes: 0.002992391586303711

30000 takes: 0.007980585098266602

40000 takes: 0.0199429988861084

50000 takes: 0.03391575813293457

70000 takes: 0.018947362899780273

80000 takes: 0.055847883224487305

90000 takes: 0.04089236259460449

100000 takes: 0.03391218185424805

Time to remove elements from Stack:

10000 takes: 0.009983301162719727

20000 takes: 0.030913829803466797

30000 takes: 0.0279233455657959

40000 takes: 0.05086517333984375

50000 takes: 0.03774094581604004

60000 takes: 0.06283450126647949

70000 takes: 0.058838844299316406

80000 takes: 0.06280803680419922

90000 takes: 0.06582164764404297

100000 takes: 0.059885501861572266

Time to add elements to StackLeft:

10000 takes: 0.08074545860290527

20000 takes: 0.23097586631774902

30000 takes: 0.4888572692871094

40000 takes: 0.9527907371520996

50000 takes: 1.3121168613433838

60000 takes: 1.972851276397705

70000 takes: 2.676400899887085

80000 takes: 3.048536777496338

90000 takes: 5.077842473983765

100000 takes: 5.5361456871032715

Time to remove elements from StackLeft:

10000 takes: 0.02091217041015625

20000 takes: 0.05186033248901367

30000 takes: 0.1226654052734375

40000 takes: 0.2274796962738037

50000 takes: 0.3652002811431885

60000 takes: 0.8326921463012695

70000 takes: 0.8500213623046875

80000 takes: 1.1882421970367432

90000 takes: 1.5454580783843994

100000 takes: 2.1574411392211914

Stack Applications

Paring parenthesis in a string:

The parentheses used for function or operation execution must be properly paired. That is, each opening parenthesis must have a corresponding closing parenthesis.

If we only consider parentheses in the expression, we can easily confirm that all parentheses are properly paired in the following pattern:

()()()()

However, it becomes more complicated when parentheses are nested:

(()()()()())

((((()))))

(()((())()))

For example, the following example contains unmatched parentheses:

(((((((())

(()))

(()()(()

The following code implements a function using a stack to determine whether a string consisting of parentheses is composed of properly paired parentheses. The usage of the stack is as follows: Starting from the left of the string, when encountering an opening parenthesis or a closing parenthesis, repeat the following actions:

Opening parenthesis: Add to the stack.
Closing parenthesis: Remove the top item from the stack.

Through these actions, three cases may occur:

The stack becomes empty before the entire string is checked: There are too many closing parentheses.
The stack is not empty after checking the entire string: There are too many opening parentheses.
Otherwise, all parentheses are properly paired.

Output:

True

False

Convert infix to postfix using a stack:

In the process of converting an infix expression to a postfix expression, the operands maintain their order, while the arrangement of operators is determined by the precedence of operators and the execution order defined by parentheses. This property is leveraged in the development of an algorithm for converting notation.

Proceeding sequentially from the left of the infix expression, we examine each operand and operator encountered. Operand elements are directly appended to the postfix expression. Operators, on the other hand, are managed using a separate stack. However, considering operator precedence and the presence of parentheses, the stack may be manipulated prior to adding the operator to it.

The reason for utilizing a stack to manage operators is to ensure proper execution order.

When a lower-priority operator is encountered compared to the one already present in the stack, it indicates that calculations related to the higher or equal priority operator in the stack should be performed first.
This necessitates the removal of those higher-priority operators from the stack and their immediate addition to the postfix expression.
Moreover, in scenarios involving parentheses, such as in expressions like (A + B) * C, opening parentheses are also pushed onto the stack.
Conversely, upon encountering a closing parenthesis, the process entails popping operators from the stack until an opening parenthesis is encountered, thereby progressively constructing the postfix expression.

Convert infix to postfix:

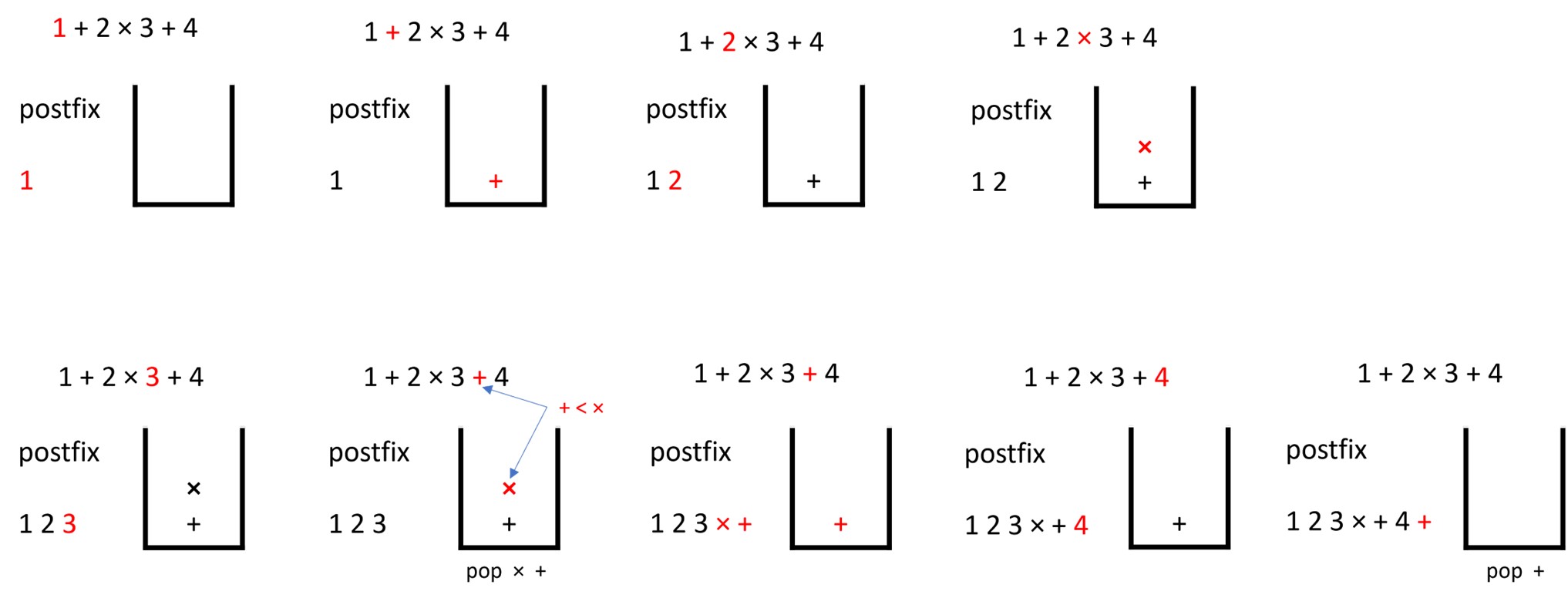
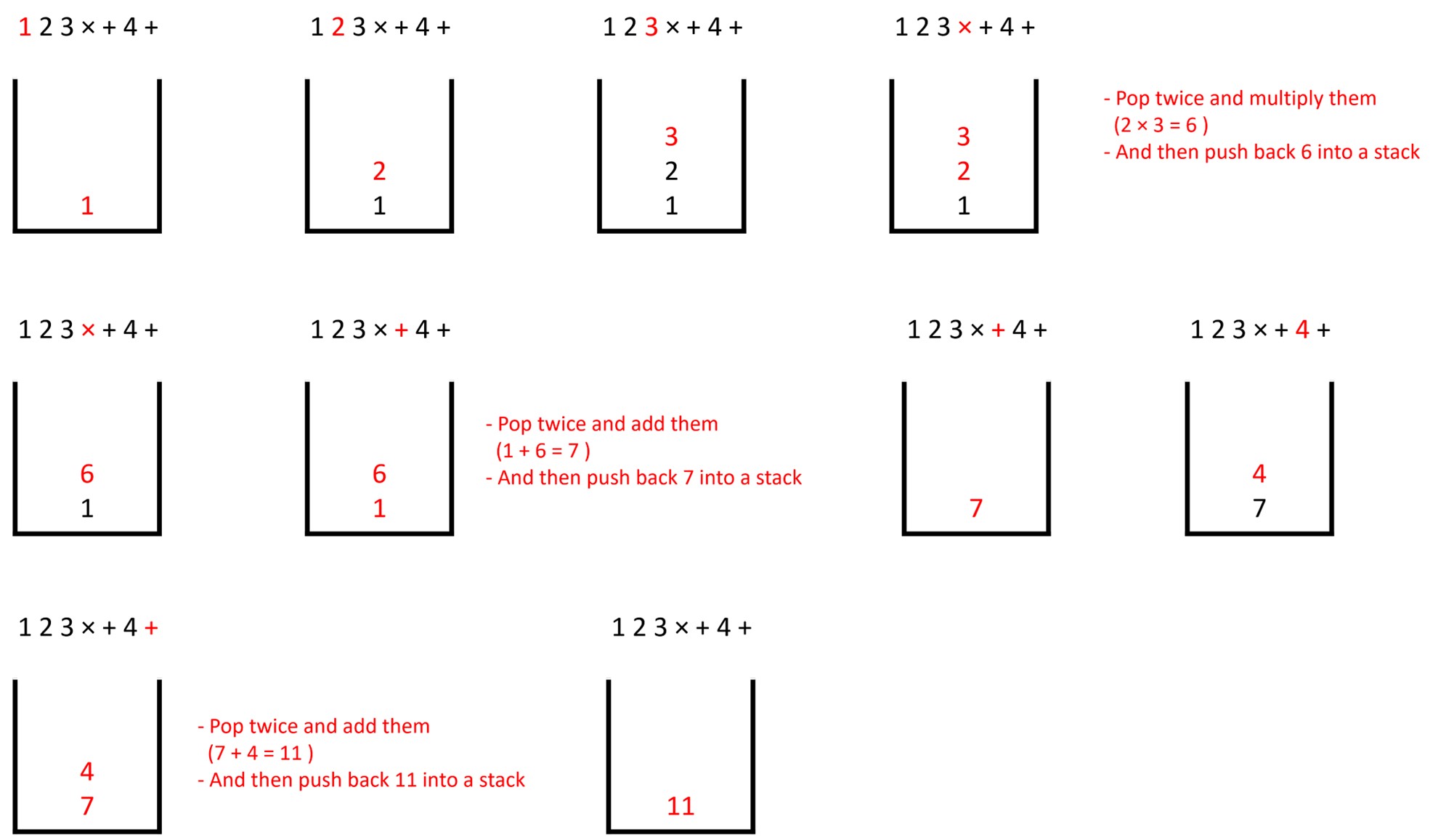
Example 1: 1 + 2 × 3 + 4

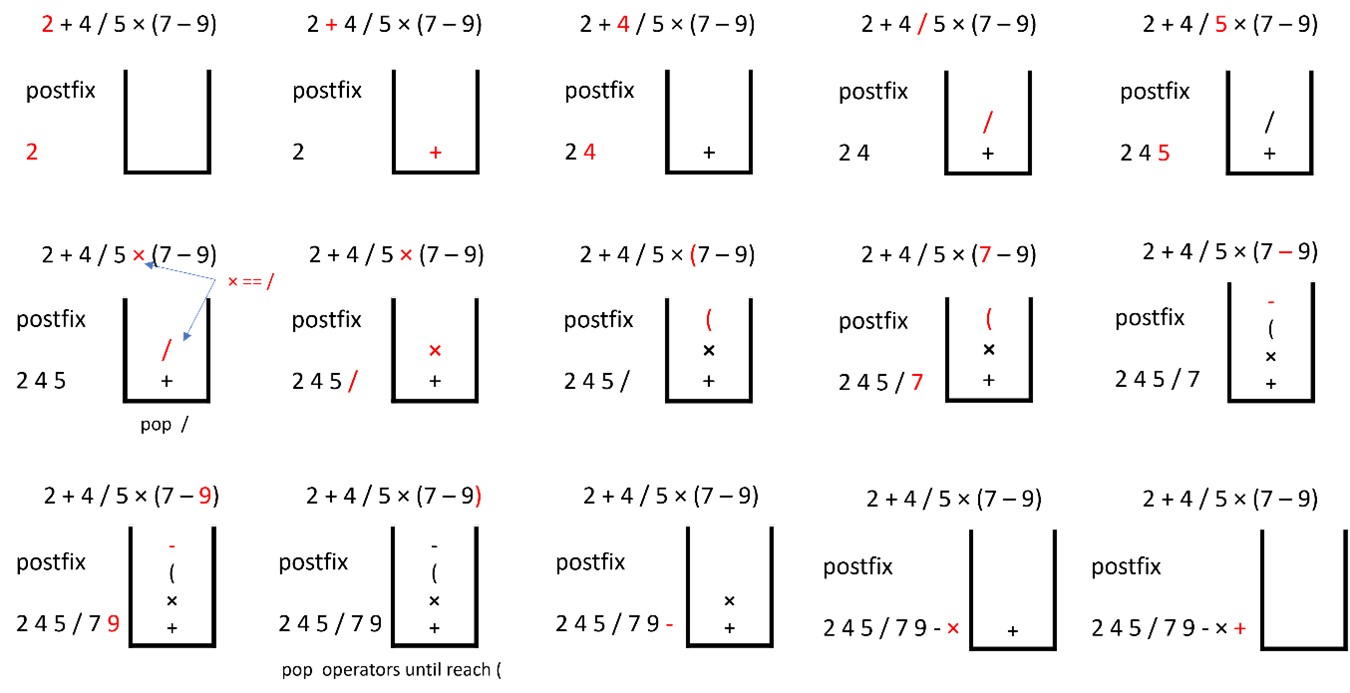
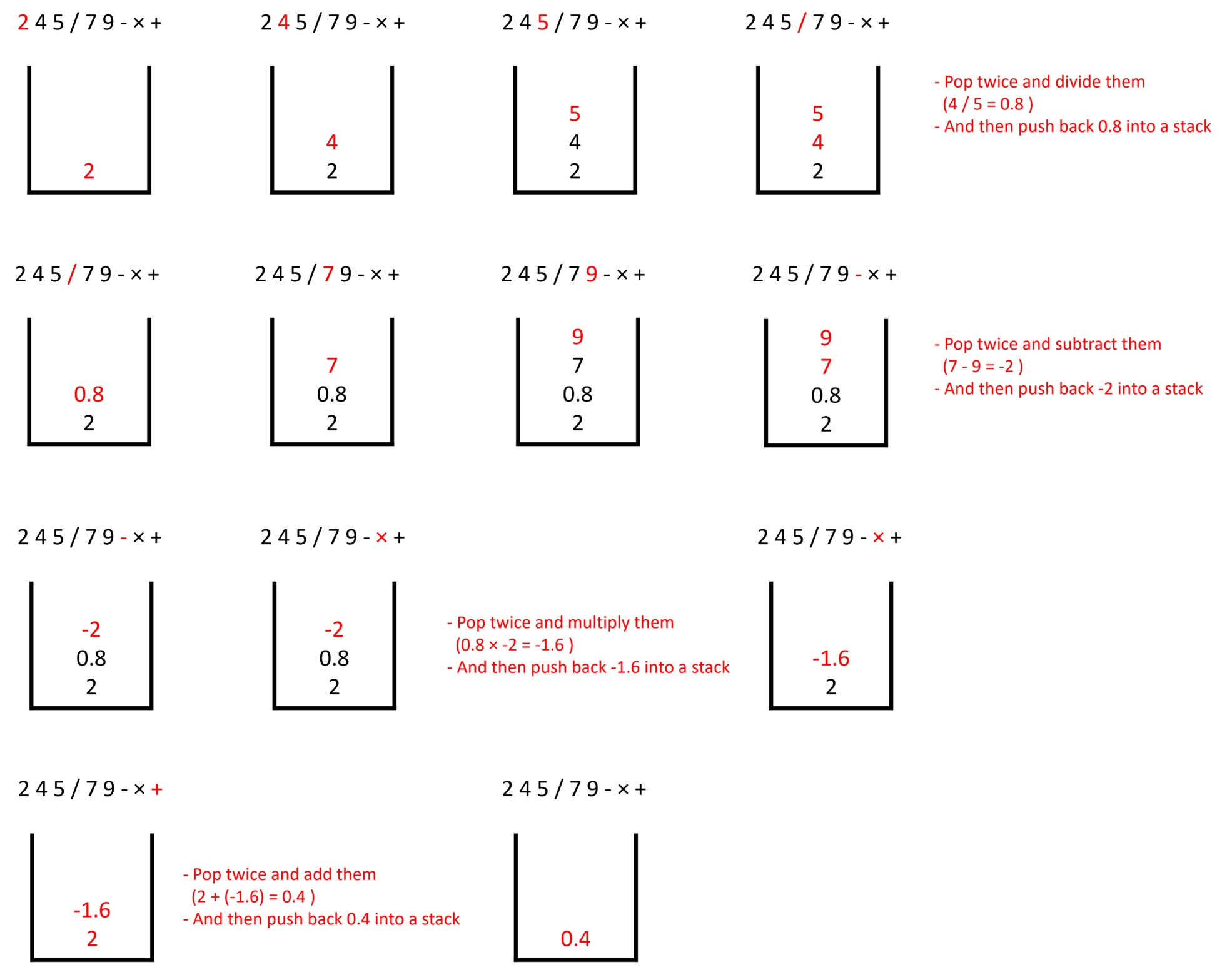
Example: 2 + 4 / 5 × (7 – 9)

Calculate using postfix

Example: 1 2 3 × + 4 +

Example: 2 4 5 / 7 9 - × +

2. Queues

A queue represents a data structure adhering to the First In First Out (FIFO) principle. A queue represents a waiting list. It can be seen as a specialized form of list where elements are inserted at the end (tail) of the queue and accessed and removed from the beginning (head) of the queue.

How it works?

Enqueue elements to a queue:

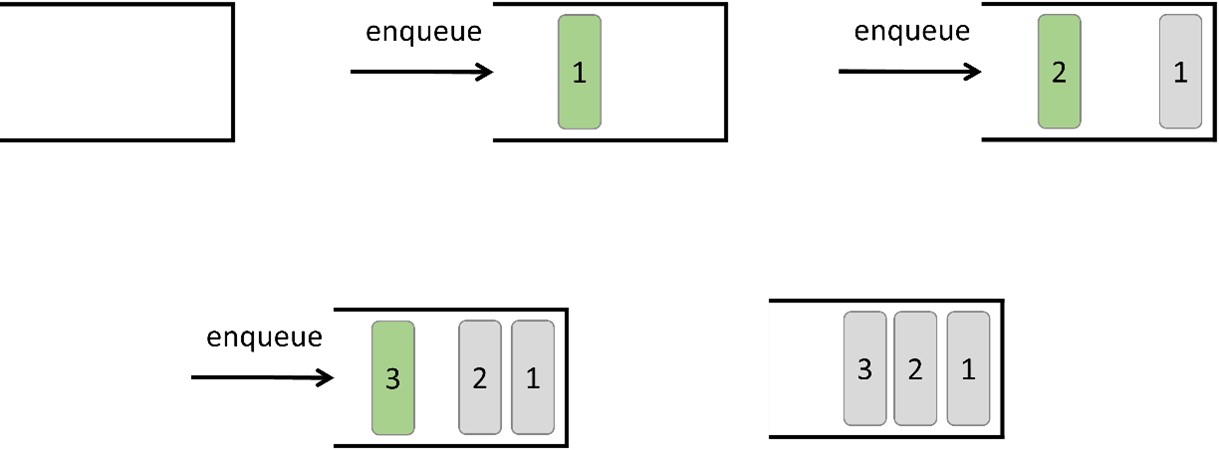
When an element (1) arrives at the queue, it is placed at the end. Subsequently, when a new element (2) arrives, it is placed after the element (1). Following this, when a new element (3) arrives, it is placed after the element (2).

Dequeue elements to a queue:

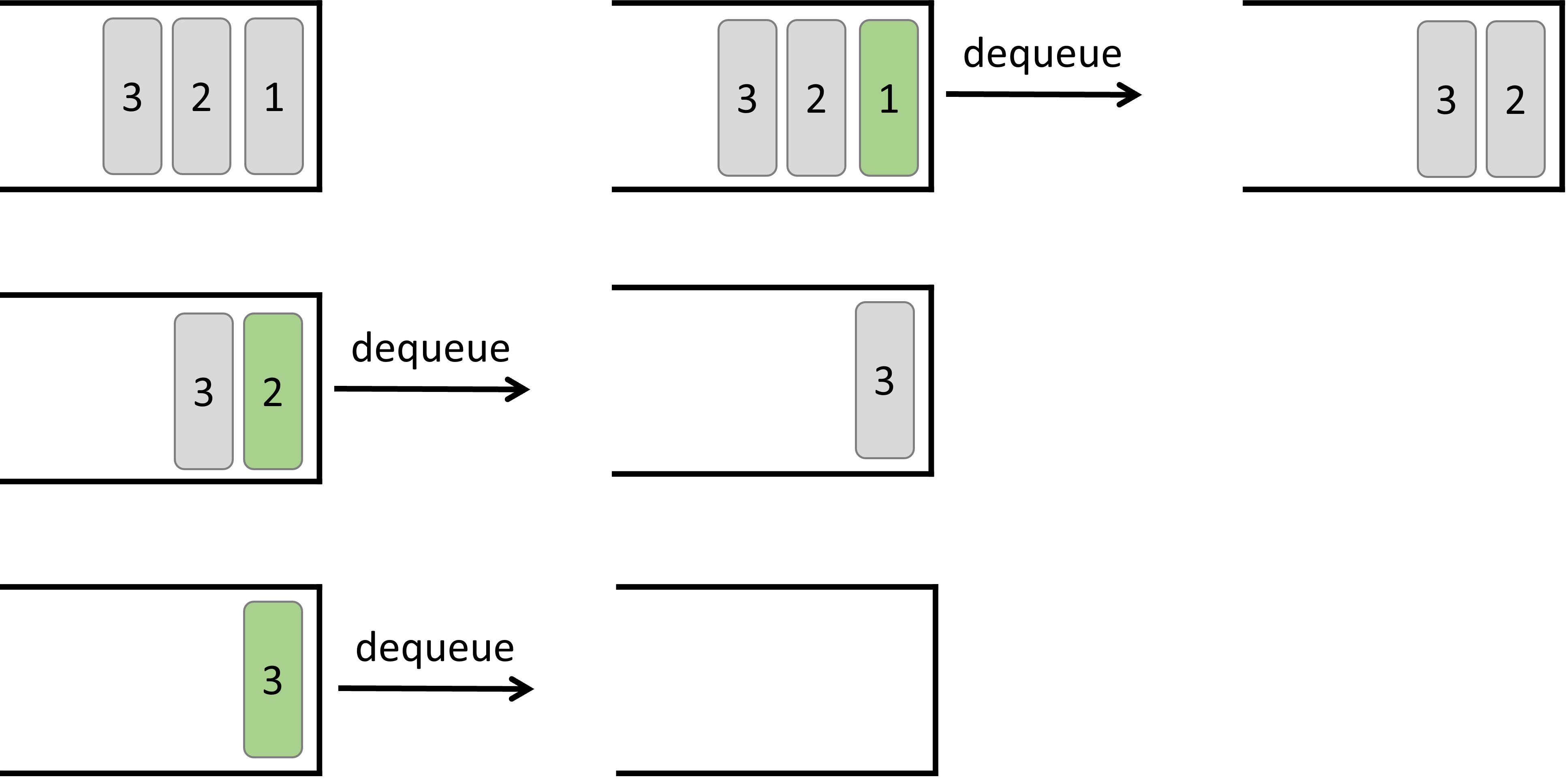
When an element is removed from a queue, the first element (1) is extracted from the queue. Subsequently, the next element (2) is removed, followed by the removal of the element (3).

Basic operations of a queue
- Enqueue: Add an element to the end of the queue
- Dequeue: Remove an element from the front of the queue
- IsEmpty: Check if the queue is empty
- getSize: Return the size of the stack

Queue Implementation

Test Program:

Output:

0 1 2 3 4 5 6 7 8 9

3. Priority Queue

In a standard queue described in the previous section, elements are managed on a First-In, First-Out basis, where they are added to the back and removed from the front.

However, a priority queue assigns priority levels to its elements. When accessing elements, those with the highest priority are dealt with first, reflecting a largest-in, first-out behavior. For instance, in a hospital's emergency room, in a hospital's emergency room, patients are prioritized with numbers, ensuring that the most urgent cases receive immediate attention.

How it works?

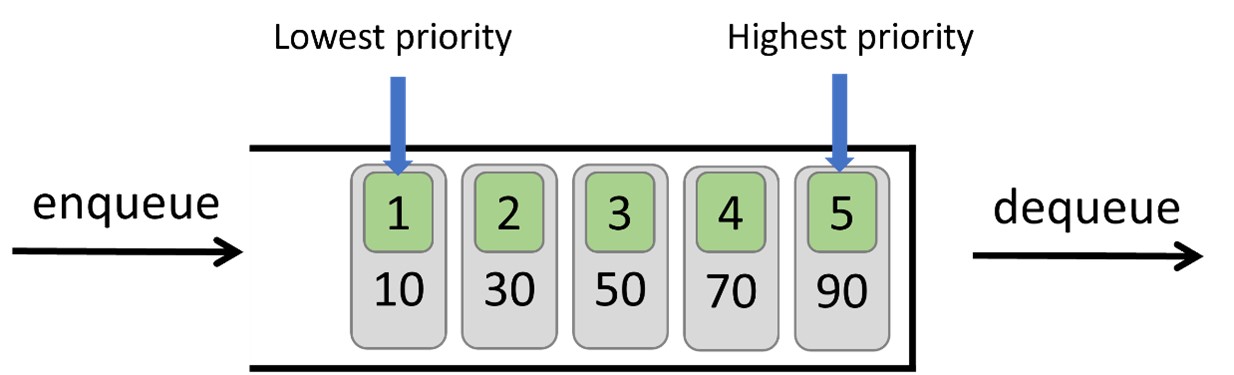
The item with the highest priority is positioned at the forefront to be served first.

Priority Queue Implementation

Using a List:

Let's suppose that 4 represents the highest priority, while 1 signifies the lowest priority.

### Using a List

class PriorityQueue:
    
    def __init__(self):
        self.queue = []

def enqueue(self, priority, item):
        self.queue.append((priority, item))
        self.queue.sort(reverse=True)  # Sort in descending order of priority

def dequeue(self):
          if not self.isEmpty():
               return self.queue.pop(0)
          else:
               raise IndexError("Cannot dequeue from an empty priorityqueue")

def getSize(self):
          return len(self.queue)

def isEmpty(self):
          return len(self.queue) == 0
    
def main():
      pq = PriorityQueue()
      pq.enqueue(2, "John")
      pq.enqueue(3, "Tom")
      pq.enqueue(1, "Kelly")
      pq.enqueue(4, "Jane")

print("Size of queue:", pq.getSize())
      print("Is queue empty?", pq.isEmpty())

print("Dequeue:", pq.dequeue())
      print("Dequeue:", pq.dequeue())
      print("Dequeue:", pq.dequeue())
      print("Dequeue:", pq.dequeue())

print("Is queue empty?", pq.isEmpty())

main()

Output:

Size of queue: 4

Is queue empty? False

Dequeue: (4, 'Jane')

Dequeue: (3, 'Tom')

Dequeue: (2, 'John')

Dequeue: (1, 'Kelly')

Is queue empty? True

Using a heapq:

Let's suppose that 4 represents the highest priority, while 1 signifies the lowest priority.

Output:

Size of queue: 4

Is queue empty? False

Dequeue: Jane

Dequeue: Tom

Dequeue: John

Dequeue: Kelly

Is queue empty? True

Using a PriorityQueue:

In this scenario, let's designate 4 as the highest priority and 1 as the lowest priority.

Output:

Size of queue: 4

Is queue empty? False

Dequeue: Jane

Dequeue: Tom

Dequeue: John

Dequeue: Kelly

Is queue empty? True

4. Deque

A deque, or double-ended queue, resembles a queue in that it's an ordered assortment of items. However, it differs in that it features two ends: a front and a rear, where items maintain their position. This structure allows for the addition of new items at either end and the removal of existing items from either end as well.

How it works?

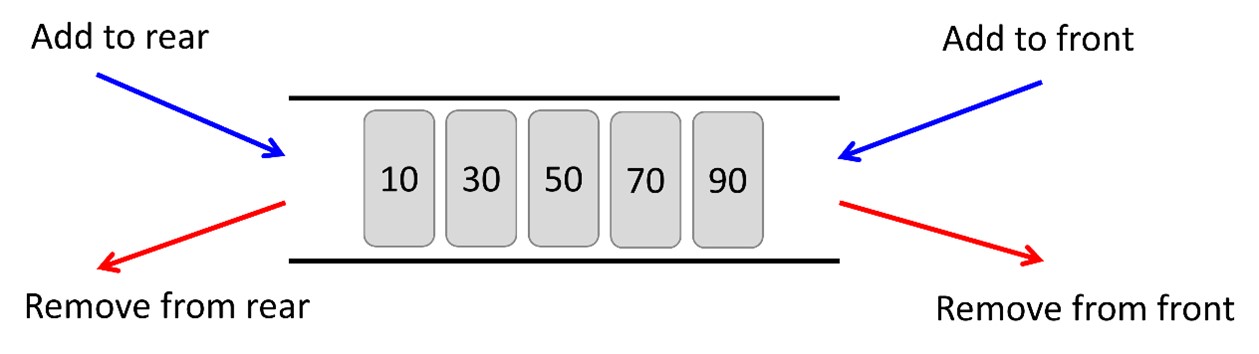
Deque Implementation

Test Program

Output:

Is empty? True

True
hawk
10
tiger

tiger
10
hawk
True

Deque Applications

Example: Palindrome

A palindrome is a word, phrase, number, or other sequence of characters that reads the same forward and backward.

To determine if a given string is a palindrome, we can create a deque object with the string. Then, we can check whether the elements at the front and the rear of the deque match each other. If they consistently match as you remove elements from both ends, the string is a palindrome.

Output:

True

False

True

False

Summary

A stack represents a linear data structure adhering to the Last In First Out (LIFO) principle. Elements are accessed, inserted, and deleted from the end, commonly referred to as the top, of the stack.
A stack can be used to convert infix to postfix.
A queue represents a data structure adhering to the First In First Out (FIFO) principle. A queue represents a waiting list. It can be seen as a specialized form of list where elements are inserted at the end (tail) of the queue and accessed and removed from the beginning (head) of the queue.
a priority queue assigns priority levels to its elements. When accessing elements, those with the highest priority are dealt with first, reflecting a largest-in, first-out behavior.
A deque, or double-ended queue, resembles a queue in that it's an ordered assortment of items. However, it differs in that it features two ends: a front and a rear, where items maintain their position. This structure allows for the addition of new items at either end and the removal of existing items from either end as well.

Programming Exercises

Exercise 1: Balanced Parentheses Checker

Write a function that takes a string containing only parentheses (,), curly braces {,}, and square brackets [,] and returns True if the parentheses are balanced and False otherwise. For example:

balanced("(())") # Output: True

balanced("({[]})") # Output: True

balanced("(()") # Output: False

Exercise 2: Evaluate Postfix Expression

Write a function to evaluate a postfix expression using a stack. The postfix expression is provided as a string with operands and operators separated by spaces. For example:

evaluate_postfix("3 4 + 2 *") # Output: 14

evaluate_postfix("5 1 2 + 4 * + 3 -") # Output: 14

Exercise 3: Interleave the First Half of Queue with Second Half

Write a function to interleave the first half of a queue with the second half. For example, if the queue is [1, 2, 3, 4, 5, 6], after interleaving it becomes [1, 4, 2, 5, 3, 6].

Exercise 4: Generate Binary Numbers from 1 to n using a Queue

Write a function to generate binary numbers from 1 to n using a queue. For example, if n is 5, the output should be ["1", "10", "11", "100", "101"].

Exercise 5: Top K Frequent Elements

Given an integer array, return the k most frequent elements. Implement it using a priority queue to efficiently find the top k frequent elements.

Exercise 6: K^th Largest Element in an Array

Find the k^th largest element in an unsorted integer array using a priority queue.

Exercise 7: Sliding Window Maximum:

Given an array of integers and a window size k, return the maximum value in each window of size k as it slides from left to right. Use a deque to efficiently find the maximum value in each window.