Learning Objectives
- Understand the concept of searching algorithms
- Gain familiarity with various searching techniques such as linear search, binary search
- Learn the implementation details of each searching algorithm
- Understand time complexity of searching algorithms
19-1. Linear Search
Linear search, also known as sequential searching, is a straightforward algorithmic approach. It begins from one end of a list and inspects each element sequentially until the desired element is located. It represents the most basic form of searching algorithm.
- How it works?
Let's say we have a list of elements, and we're attempting to find a specific element, which we'll refer to as the "key."

The following steps are as follows to find key = 3.
Step 1: We begin by comparing the first element in the list, which is '5', with the key. Since the key, which is 3, is not equal to 5, we move on to the next element.


(3 ≠ 5)
Step 2: Next, we compare the second element in the list, which is '8', with the key. Since the key, which is 3, is not equal to 8, we proceed to the next element.


(3 ≠ 8)
Step 3: Next, we compare the third element in the list, which is '10', with the key. Since the key, which is 3, is not equal to 10, we proceed to the next element.


(3 ≠ 10)
Step 4: Next, we compare the fourth element in the list, which is '3', with the key. Since the key, which is 3, is equal to 3, we found the element.


KEY
Otherwise, if the key is not found, it indicates that the key does not exist within the list.
- Linear Search Implementation
Example 1: Search for a number
Output:
| 3 is found at index 3 |
Example 2: Search for a string
Output:
| Lee is found at index 3 |
- Time Complexity
In the linear Search, every element should be compared at least once. In the best-case scenario, the complexity is when the key is found at the first index. Conversely, in the worst-case scenario, the complexity is when the key is either found at the last index or not found at all.
19-2. Binary Search
Binary search is another widely used approach for searching within a list of values. However, for binary search to function correctly, it requires that the elements in the list are already ordered. Assume that the list is in ascending order.
- How it works
To begin, we must designate three indices: 'low', 'mid', and 'high'. 'low' corresponds to the smallest element, 'high' to the largest, and 'mid' is calculated as "(low + high) / 2". We are attempting to find a specific element, which we'll refer to as the "key."





Low Mid High
Example 1
The following steps are as follows to find key = 31.
Step 1: We begin by comparing the 'mid' element in the list, which is '19', with the key. Since the key, which is 31, is not equal to 19 and greater than 19.
31 ≠ 19





Low = 0 Mid = 3 High = 6
In Step 2, since the key (31) is greater than 19, we don't need to search the half of the list that is less than the key. Therefore, we update the 'low' and 'mid' indices as follows: 'low = mid + 1 = 3 + 1 = 4', so 'low' indicates 23. 'mid = (low + high) / 2 = (4 + 6) / 2 = 5', which indicates 31. 'high' remains unchanged.
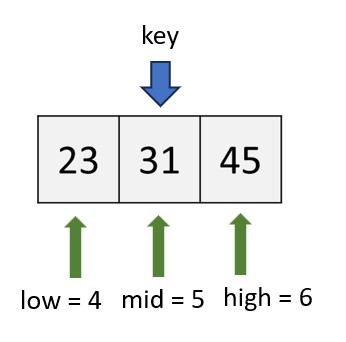
Step 3: Moving forward, we assess the 'mid' element within the list, denoted as '31', in comparison to the key value, which is also 31. Given that the key matches the value of 31, we have successfully identified the desired element.
Example 2
The following steps are as follows to find key = 10.
Step 1: We begin by comparing the 'mid' element in the list, which is '19', with the key. Since the key, which is 10, is not equal to 19 and less than 19.
10 ≠ 19





Low=0 Mid=3 High=6
In Step 2, since the key (10) is less than 19, we don't need to search the half of the list that is greater than the key. Therefore, we update the 'mid' and 'high' indices as follows: 'high = mid - 1 = 3 - 1 = 2', so 'high' indicates 15. 'mid = (low + high) / 2 = (0 + 2) / 2 = 1', which indicates 12. 'low' remains unchanged.
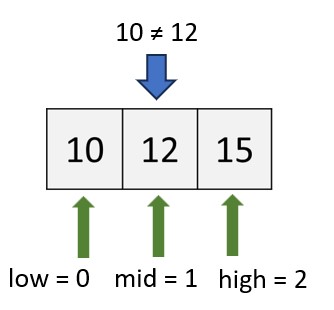
Step 3: Next, we compare the 'mid' element in the list, which is '12', with the key. Since the key, which is 10, is not equal to 12 and less than 12. And update indices as below: 'high = mid - 1 = 1 - 1 = 0', so 'high' indicates 10. 'mid = (low + high) / 2 = (0 + 1) / 2 = 0', which indicates 10. 'low' remains unchanged.
Step 4: Moving forward, we assess the 'mid' element within the list, denoted as '10', in comparison to the key value, which is also 10. Given that the key matches the value of 10, we have successfully identified the desired element.
- Binary Search Implementation
Example: 1 Search for a number
Output:
| 31 is found at index 5 |
Example 2: Search for a string
Output:
| Davis is found at index 0 |
- Time Complexity
Let T(n) represent the time complexity for a binary search on a list of n elements. With each comparison, the number of elements is halved.
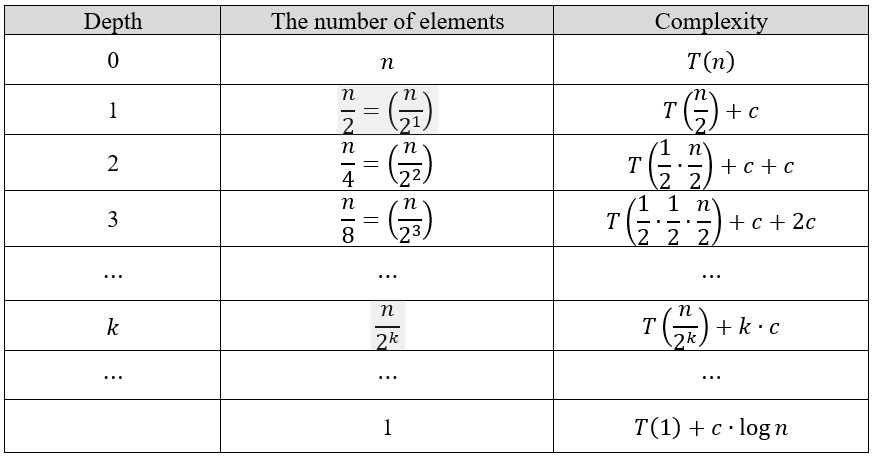
Until the key value is found, indicating that only one element remains, the relationship holds true, where represents the initial number of elements and represents the number of comparisons made. By solving for in terms of , we find .
Therefore, the number of comparisons made is logarithmic with respect to the initial number of elements, leading to a time complexity of O(log n).
Summary
- Linear searching algorithm sequentially checks each element in a list until the target element is found.
- Linear searching is suitable for small lists or unsorted data.
- Time complexity of linear searching is O(n).
- Binary searching algorithm requires a sorted list.
- Binary searching algorithm divides the list in half at each step and compares the target element with the middle element to determine if it lies in the first or second half of the list.
- Time complexity of binary searching algorithms is O(log n).
Programming Exercises
Exercise 1: Find Maximum Element in a List
Write a Python function that uses linear search to find the maximum element in a list.
Exercise 2: Find Duplicates in a List
Write a Python function that uses searching algorithms to find duplicate elements in a list and returns a list of duplicates.
Exercise 3: Search for a Key in a Dictionary
Write a Python function that takes a dictionary and a key as input and checks if the key exists using linear search.
Exercise 4: Check if a String is a Palindrome
Implement a Python function that uses two pointers to check if a given string is a palindrome by comparing characters from the start and end of the string.
Exercise 5: Search for a Word in a Text File
Implement a Python program that reads a text file and searches for a specific word, counting how many times it appears.
Exercise 6: Phone Book Search
Implement a simple phone book application using Python dictionaries. Write functions to add contacts, search for a contact by name, and delete contacts. Utilize linear search for searching contacts by name.
Exercise 7: Application of Searching Algorithms
Given a list of integers, implement a function find_pair_sum(arr, target_sum) that uses any of the searching algorithms to find a pair of numbers in the list that sum up to the target_sum. Return the indices of the pair if found, otherwise return None.